Ctrl+K

Limit

3. Limit#

3.1. Domain of functions#

a. Denominator cannot be 0 i. The domain of \(f(x) = \frac{1}{\sqrt{x^2 - 9}} \to x < -3 \land x > 3\)

b. Roots of even squared are greater than or equal to 0

c. The number of logarithm is greater than 0 (\(\ln x \to x > 0\))

d. Arcsin \(x\) and Arccos \(x \to x \leq 1\)

3.1.1. The equivalent of functions#

The same domain and the same mapping

i. \(f(x) = \ln(x - 1) \neq g(x) = \ln\sqrt{(x - 1)^2}\)

ii. \(f(x) = \frac{x}{x} \neq g(x) = 1\)

iii. \(f(x) = \sqrt{x^2} = g(x) = |x|\)

iv. \(f(x) = \begin{cases} -x, & x \geq 1 \\ 1, & x < 1 \end{cases} \neq g(x) = \begin{cases} 0, & x = 1 \\ 1, & x < 1 \end{cases}\)

3.1.2. The definition of limit#

Let \(f(x)\) be a function defined on an interval that contains \(x = a\), except possibly at \(x = a\). Then we say that,

\[ \lim_{x \to a} f(x) = L \]

if for every number \(\epsilon > 0\) there is some number \(\delta > 0\) such that

\[ |f(x) - L| < \epsilon \quad \text{whenever} \quad 0 < |x - a| < \delta \]

3.2. Solve the limit Problem#

3.2.1. Substitute Directly#

3.2.2. L’Hopital’s Law#

i. Infinity to infinity

ii. Infinity small to infinity small

\[ \lim_{x \to 1} \frac{x - 1}{x^2 - 1} = \lim_{x \to 1} \frac{1}{2x} = \frac{1}{2} \]

3.2.3. The Property of infinity (∞) and infinity small (0)#

The product of infinity small with bounded function (e.g., \(\sin x \), \(\cos x \), \(\arctan x \), \(arccot x \)) is infinity small.

\[ \lim_{x \to \infty} \frac{\sin x}{x} = \lim_{x \to \infty} \sin x \ast \frac{1}{x} = 0 \]
\[ \lim_{x \to 2} (x - 2) \sin \frac{1}{x - 2} = \lim_{u \to \infty} \frac{\sin u}{u} = 0 \]

3.2.4. Three special cases#

Factorization

\[ \lim_{x \to 1} \frac{x - 1}{x^2 - 1} = \lim_{x \to 1} \frac{1}{x + 1} = \frac{1}{2} \]
\[ \lim_{x \to 4} \frac{x - 4}{\sqrt{x + 5} - 3} = \lim_{x \to 4} \frac{\sqrt{x + 5} + 3}{x + 5 - 9} = \lim_{x \to 4} \sqrt{x + 5} + 3 = 6 \]

Rationalization of numerator and denominator

\[ \lim_{x \to 4} \frac{x - 4}{\sqrt{x + 5} - 3} = \lim_{x \to 4} \frac{(x - 4)(\sqrt{x + 5} + 3)}{(\sqrt{x + 5} - 3)(\sqrt{x + 5} + 3)} \]

Get the highest order \(x\to \infty\)

\[ \lim_{x \to \infty} \frac{2x^3 + 3x^2 + 5}{7x^3 + 4x^2 - 1} = \frac{2}{7} \]
\[ \lim_{x \to \infty} \frac{3x^2 + 5}{7x^3 + 4x^2 - 1} = 0 \]
\[ \lim_{x \to \infty} \frac{2x^3 + 3x^2 + 5}{4x^2 - 1} = \infty \]

3.3. Two important limit#

i. \(\lim_{u(x) \to 0} \frac{\sin u(x)}{u(x)} = 1\)

  1. Prove using the definition of differential

    a) \(\lim_{x \to 0} \sin x = x\)

    \[ f'(x) = \frac{f(x + \delta) - f(x)}{\delta} \to f(x + \delta) = f(x) + f'(x) \ast \delta, \text{ when } \delta \to 0 \]

    \(\sin (x + \delta) \approx \sin x + \cos x \ast \delta\) when \(\delta \to 0\)

    \(\sin \delta \approx 0 + \delta\), when \(\delta \to 0\)

    Replace \(\delta\) with \(x\), \(\lim_{x \to 0} \sin x = x\)

ii. \(\lim_{A \to \infty} \left(1 + \frac{1}{A}\right)^A = e\)

  1. Prove using Taylor’s Formula

    \[ e < \left(1 + \frac{1}{k}\right)^k = 1 + \frac{k}{1} \left(\frac{1}{k}\right)^1 + \frac{k(k - 1)}{1 \cdot 2} \left(\frac{1}{k}\right)^2 + \frac{k(k - 1)(k - 2)}{1 \cdot 2 \cdot 3} \left(\frac{1}{k}\right)^3 + \cdots \]

    a)

    \[ e = 1 + \frac{1}{2!} + \frac{1}{3!} + \cdots = e \]

  2. \(\lim_{x \to \infty} \left(1 - \frac{2}{x}\right)^x = e^{-2} = \frac{1}{e^2}\)

  3. \(\lim_{x \to 0} (1 - 2x)^{\frac{1}{x}} = e^{-2}\)

  4. \(\lim_{x \to \infty} \left(1 + \frac{1}{n}\right)^{n+3} = e\)

3.4. Equivalence of infinity small#

i. \(\lim_{x \to 0} \frac{\sin x}{x} = 1 \to \sin x \sim x \ (\text{when } x \to 0)\)

ii. \(1 - \cos x \sim \frac{1}{2} x^2\)

  1. Prove: \(\lim_{x \to 0} \frac{1 - \cos x}{\frac{1}{2}x^2} = \frac{\sin x}{x} = 1\)

iii. \(\ln(1 + x) \sim x\)

  1. Prove: \(\ln(1 + x + \delta) = \ln(1 + x) + \frac{\delta}{1 + x} = \ln 1 + \delta \to \ln(1 + \delta) \approx \delta \text{ when } \delta \to 0 \text{ and } x = 0\)

  2. \(\lim_{x \to 0} \frac{\ln(1 + x)}{\sin 3x} = \frac{2x}{3x} = \frac{2}{3}\)

iv. \(e^x - 1 \sim x\)

v. \((1 + x)^\alpha = 1 + \alpha x\)

  1. Prove: \((1 + x + \delta)^\alpha = (1 + x)^\alpha + (\alpha \delta)(1 + x)^{\alpha - 1} \to (1 + \delta)^\alpha = 1 + \alpha \delta \text{ when } \delta \to 0 \text{ and } x = 0\)

3.5. Continuous#

3.5.1. Continuous in functions#

  1. \(f(x)\) has a definition at \(x_0\)

  2. \(\lim_{x \to x_0} f(x) = f(x_0)\)

3.5.2. Example#

\(f(x) = \begin{cases} x^2 + 2a, & x \leq 0, \\ \frac{\sin x}{2x}, & x > 0 \end{cases}\)

is continuous at \(x = 0\), what’s the value of \(a\)?

Answer

\(\lim_{x \to 0} (x^2 + 2a) = 2a\), \(\lim_{x \to 0} \frac{\sin x}{2x} = \frac{1}{2} = 2a \to a = \frac{1}{4}\)

3.6. The break points of functions#

  1. The point with invalid definition

  2. The point with no limits

    a. \(x = 3\) for \(f(x) = \frac{x^2 + 1}{x - 3}\), with limit \(= \infty\)

  3. The point with limit that does not equal to its function value

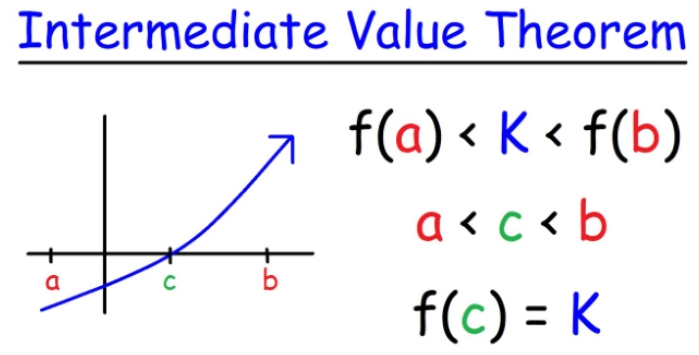
3.7. The Intermediate Value Theorem#

If \(f(x)\) is continuous on the closed interval \([a, b]\) and \(k\) is any number between \(f(a)\) and \(f(b)\), then there exists at least one value \(c\) in the interval \((a, b)\) such that \(f(c) = k\).

a. Prove there is a solution of \(x^3 - 4x^2 + 1 = 0\) on the interval \((0,1)\).

image.png

Contents