2. Matrix Mutiplication
\[
A_{m \times n} \ast B_{n \times p} = C_{m \times p}
\]
2.1. Interpret by column
\[\begin{split}
\begin{bmatrix}
2 & 7 \\
3 & 8 \\
4 & 9
\end{bmatrix}
\begin{bmatrix}
1 & 6 \\
0 & 1
\end{bmatrix}
=
\begin{bmatrix}
\begin{bmatrix} 2 & 7 \\ 3 & 8 \\ 4 & 9 \end{bmatrix}
\begin{bmatrix} 1 \\ 0 \end{bmatrix},
\begin{bmatrix} 2 & 7 \\ 3 & 8 \\ 4 & 9 \end{bmatrix}
\begin{bmatrix} 6 \\ 1 \end{bmatrix}
\end{bmatrix}
=
\begin{bmatrix}
1 \ast \begin{bmatrix} 2 \\ 3 \\ 4 \end{bmatrix} + 0 \ast \begin{bmatrix} 7 \\ 8 \\ 9 \end{bmatrix},
6 \ast \begin{bmatrix} 2 \\ 3 \\ 4 \end{bmatrix} + 1 \ast \begin{bmatrix} 7 \\ 8 \\ 9 \end{bmatrix}
\end{bmatrix}
\end{split}\]
2.2. Interpret by row
\[\begin{split}
\begin{bmatrix}
2 & 7 \\
3 & 8 \\
4 & 9
\end{bmatrix}
\begin{bmatrix}
1 & 6 \\
0 & 1
\end{bmatrix}
=
\begin{bmatrix}
\begin{bmatrix} 2 & 7 \end{bmatrix} \begin{bmatrix} 1 & 6 \\ 0 & 1 \end{bmatrix} \\
\begin{bmatrix} 3 & 8 \end{bmatrix} \begin{bmatrix} 1 & 6 \\ 0 & 1 \end{bmatrix} \\
\begin{bmatrix} 4 & 9 \end{bmatrix} \begin{bmatrix} 1 & 6 \\ 0 & 1 \end{bmatrix}
\end{bmatrix}
=
\begin{bmatrix}
2 \ast \begin{bmatrix} 1 & 6 \end{bmatrix} + 7 \ast \begin{bmatrix} 0 & 1 \end{bmatrix} \\
3 \ast \begin{bmatrix} 1 & 6 \end{bmatrix} + 8 \ast \begin{bmatrix} 0 & 1 \end{bmatrix} \\
4 \ast \begin{bmatrix} 1 & 6 \end{bmatrix} + 9 \ast \begin{bmatrix} 0 & 1 \end{bmatrix}
\end{bmatrix}
\end{split}\]
2.3. Another mutiplication rule
\[\begin{split}
\begin{bmatrix}
2 & 7 \\
3 & 8 \\
4 & 9
\end{bmatrix}
\begin{bmatrix}
1 & 6 \\
0 & 1
\end{bmatrix}
\end{split}\]
E.g.
\[\begin{split}
\begin{bmatrix}
2 & 3 \\
3 & 18 \\
4 & 24
\end{bmatrix}
=
\begin{bmatrix}
2 & 12 \\
3 & 18 \\
4 & 24
\end{bmatrix},
\end{split}\]
it fits our rule: the columns of \(C\) are combinations of columns of \(A\), and rows of \(C\) are combinations of rows of \(B\).
Since
$\(
\begin{bmatrix}
2 & 12 \\
3 & 18 \\
4 & 24
\end{bmatrix}
\)$
can be decomposed as two \(3 \times 1\) and \(1 \times 2\) matrices, we can see that no matter the column space or row space,
\[\begin{split}
\begin{bmatrix}
2 & 12 \\
3 & 18 \\
4 & 24
\end{bmatrix}
\end{split}\]
is a line.
Therefore, \(AB = \text{sum of (columns of } A \times \text{ rows of } B)\)
\[\begin{split}
\begin{bmatrix}
2 & 7 \\
3 & 8 \\
4 & 9
\end{bmatrix}
\begin{bmatrix}
1 & 6 \\
0 & 1
\end{bmatrix}
=
\begin{bmatrix}
2 & 3 \\
3 & 4 \\
4 & 9
\end{bmatrix}
\begin{bmatrix}
1 & 6
\end{bmatrix}
+
\begin{bmatrix}
7 \\
8 \\
9
\end{bmatrix}
\begin{bmatrix}
0 & 1
\end{bmatrix}
=
\begin{bmatrix}
2 \times 6 + 7 \\
3 \times 6 + 8 \\
4 \times 6 + 9
\end{bmatrix}
\end{split}\]
2.4. The Laws for Matrix Operations
2.4.1. About addition
\[
A + B = B + A \quad \text{(commutative law)}
\]
\[
c(A + B) = cA + cB \quad \text{(distributive law)}
\]
\[
A + (B + C) = (A + B) + C \quad \text{(associative law)}
\]
2.4.2. About multiplication
\[
AB \neq BA \quad \text{(the commutative "law" is usually broken)}
\]
\[
A(B + C) = AB + AC \quad \text{(distributive law from the left)}
\]
\[
(A + B)C = AC + BC \quad \text{(distributive law from the right)}
\]
\[
A(BC) = (AB)C \quad \text{(associative law for } ABC \text{) (parentheses not needed)}
\]
2.4.3. About Powers
\[
A^p = AAA \cdots A \quad (p \text{ factors})
\]
\[
(A^p)(A^q) = A^{p+q}
\]
\[
(A^p)^q = A^{pq}.
\]
2.5. Block multiplication
If \(A\) can be divided into 4 blocks of matrices, \(A_1, A_2, A_3, A_4\), and \(B\) as \(B_1, B_2, B_3, B_4\), then
\[\begin{split}
\begin{bmatrix}
A_1 & A_2 \\
A_3 & A_4
\end{bmatrix}
\begin{bmatrix}
B_1 & B_2 \\
B_3 & B_4
\end{bmatrix}
=
\begin{bmatrix}
A_1B_1 + A_2B_3 & \cdots \\
\cdots & \cdots
\end{bmatrix}
\end{split}\]
Just like regular matrix multiplication.
2.6. Inverse
For rectangular matrices, the left inverse is not equal to the right inverse, but for a square matrix,
\[
A^{-1}A = I = AA^{-1}
\]
2.6.1. Example
\[\begin{split}
\begin{bmatrix}
1 & 3 \\
2 & 7
\end{bmatrix}
\begin{bmatrix}
a & c \\
b & d
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
\to
\begin{bmatrix}
a & c \\
b & d
\end{bmatrix}
=
\begin{bmatrix}
7 & -3 \\
-2 & 1
\end{bmatrix}
\end{split}\]
2.6.2. property

2.7. Two ways to solve the inverse
2.7.1. Solve them by the meaning
\[\begin{split}
\begin{bmatrix}
1 & 3
\end{bmatrix}
\begin{bmatrix}
a \\
b
\end{bmatrix}
=
\begin{bmatrix}
1 \\
0
\end{bmatrix}
\rightarrow a + 3b = 1 \rightarrow a = 7, b = -2
\end{split}\]
\[\begin{split}
\begin{bmatrix}
2 & 7
\end{bmatrix}
\begin{bmatrix}
a \\
b
\end{bmatrix}
=
\begin{bmatrix}
1 \\
0
\end{bmatrix}
\rightarrow 2a + 7b = 0
\end{split}\]
\[\begin{split}
\begin{bmatrix}
1 & 3
\end{bmatrix}
\begin{bmatrix}
c \\
d
\end{bmatrix}
=
\begin{bmatrix}
0 \\
1
\end{bmatrix}
\rightarrow c + 3d = 0 \rightarrow c = -3, d = 1
\end{split}\]
\[\begin{split}
\begin{bmatrix}
2 & 7
\end{bmatrix}
\begin{bmatrix}
c \\
d
\end{bmatrix}
=
\begin{bmatrix}
0 \\
1
\end{bmatrix}
\rightarrow 2c + 7d = 1
\end{split}\]
2.7.2. Gauss -Jordan (Augmented matrix)
\[\begin{split}
\begin{bmatrix}
1 & 3 & 1 & 0 \\
2 & 7 & 0 & 1
\end{bmatrix}
\to
\begin{bmatrix}
1 & 3 & 1 & 0 \\
0 & 1 & -2 & 1
\end{bmatrix}
\to
\begin{bmatrix}
1 & 0 & 7 & -3 \\
0 & 1 & -2 & 1
\end{bmatrix}
\end{split}\]
\[
E \begin{bmatrix} A \mid I \end{bmatrix} = \begin{bmatrix} I \mid A^{-1} \end{bmatrix}, \quad E \text{ is the elimination matrix}
\]
2.8. Singular matrix (do not have inverse)
\[\begin{split}
\begin{bmatrix}
1 & 3 \\
2 & 6
\end{bmatrix}
\end{split}\]
Square matrices do not have an inverse if I can find a vector \(\mathbf{x}\) with \(A\mathbf{x} = 0\).
\[\begin{split}
\begin{bmatrix}
1 & 3 \\
2 & 6
\end{bmatrix}
\begin{bmatrix}
3 \\
-1
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0
\end{bmatrix}
\end{split}\]
2.9. Important Example
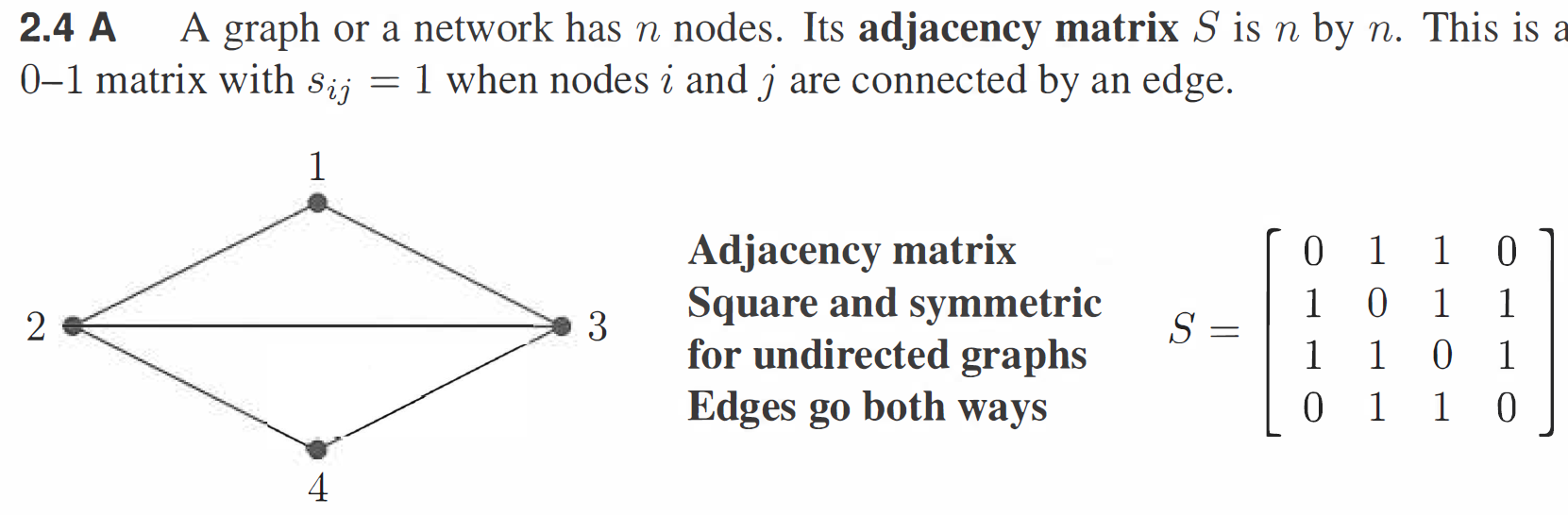
The matrix \(S^2\) has a useful interpretation. \((S^2)_{ij}\) counts the walks of length 2 between node \(i\) and node \(j\). Between nodes 2 and 3, the graph has two walks: go via 1 or go via 4. From node 1 to node 1, there are also two walks: 1→2→1 and 1→3→1.
\[\begin{split}
S^2 =
\begin{bmatrix}
2 & 1 & 1 & 2 \\
1 & 3 & 2 & 1 \\
1 & 2 & 1 & 2 \\
2 & 1 & 1 & 2
\end{bmatrix}
\quad
S^3 =
\begin{bmatrix}
2 & 5 & 5 & 2 \\
5 & 4 & 5 & 5 \\
5 & 5 & 4 & 5 \\
2 & 5 & 5 & 2
\end{bmatrix}
\end{split}\]
Can you find 5 walks of length 3 between nodes 1 and 2?
The real question is why \(S^N\) counts all the \(N\)-step paths between pairs of nodes. Start with \(S^2\) and look at matrix multiplication by dot products:
\[(S^2)_{ij} = \text{(row } i \text{ of } S) \cdot \text{(column } j \text{ of } S) = s_{i1}s_{1j} + s_{i2}s_{2j} + s_{i3}s_{3j} + s_{i4}s_{4j}. \quad (7)\]
If there is a 2-step path \(i \to 1 \to j\), the first multiplication gives \(s_{i1}s_{1j} = (1)(1) = 1\). If \(i \to 1 \to j\) is not a path, then either \(i \to 1\) is missing or \(1 \to j\) is missing. So the multiplication gives \(s_{i1}s_{1j} = 0\) in that case.




