Ctrl+K

Matrix Interpretation

1. Matrix Interpretation#

1.1. Interpretation of equation sets#

  • Suppose we have the following equation sets

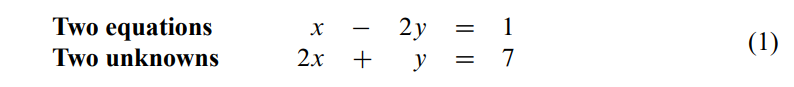
image.png

1.1.1. Row Picture#

  • Hard to draw when dimensions goes beyond 2

image.png

1.1.2. Column Picture#

  • Linear Combination of Columns

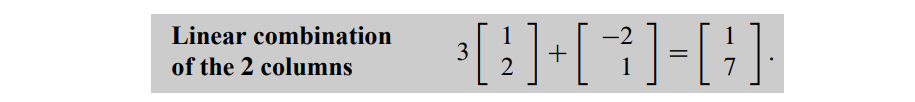
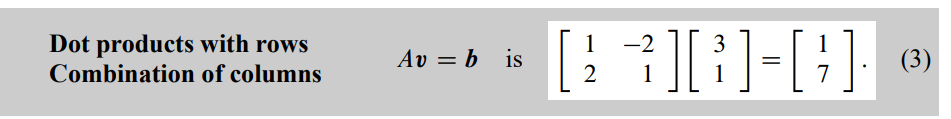
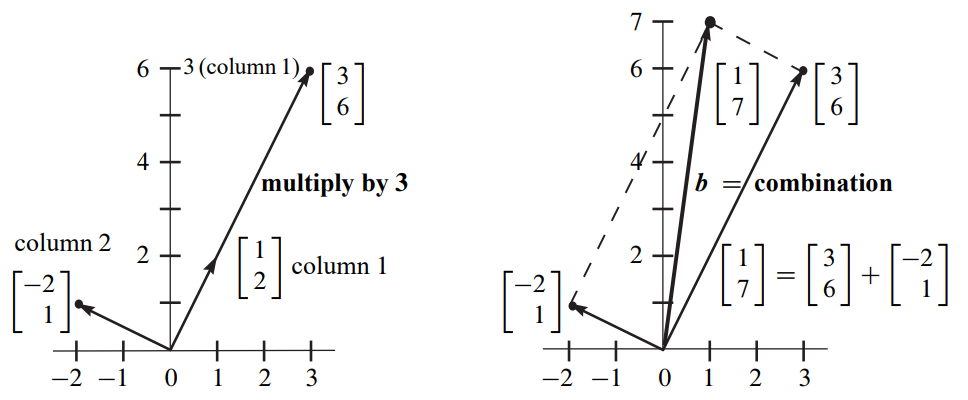
    image.png

    image.png

    image.png

    image.png

1.1.3. Quiz#

Q: Can I solve \( Av = b \) for every \( b \)? (means, Do the linear combination of the columns fill 3D space?)

My Answer: Yes, if vectors in \( A \) are not parallel, then they can be the basis for 3D space.

Professor’s Answer: If those three vectors lie within the same plane (which means you can get one vector from the linear combination of the other two vectors), then they can only form a plane instead of a 3D space.

1.2. Elimination#

  • A systematic way to solve the solution

1.2.1. Upper triangular matrix#

The most important purpose in elimination is from \(A→U\)(upper triangular matrix )

1.2.2. Augmented matrix#

  • Add y (response) into the x’s (parameters’) matrix

Method of Gaussian Elimination 3x3 Example

Given the system of equations:

\[\begin{split} \begin{align*} 4x - 3y + z &= -8 \\ -2x + y - 3z &= -4 \\ x - y + 2z &= 3 \end{align*} \end{split}\]

  1. We start with the augmented matrix:

\[\begin{split} \begin{bmatrix} 4 & -3 & 1 & | & -8 \\ -2 & 1 & -3 & | & -4 \\ 1 & -1 & 2 & | & 3 \end{bmatrix} \end{split}\]

  1. Perform row operations to reduce to the row echelon form:

\[\begin{split} \begin{bmatrix} 1 & -1 & 2 & | & 3 \\ 0 & -1 & 2 & | & 3 \\ 0 & 1 & -7 & | & -20 \end{bmatrix} \end{split}\]

  1. Further reducing to:

\[\begin{split} \begin{bmatrix} 1 & 0 & 0 & | & -2 \\ 0 & 1 & 0 & | & 1 \\ 0 & 0 & 1 & | & 3 \end{bmatrix} \end{split}\]

  1. This yields the solution:

\[\begin{split} \begin{align*} x &= 2 \\ y &= 1 \\ z &= 3 \end{align*} \end{split}\]

1.2.3. Failure of Elimination#

  • Some pivot become 0, which means there are some vectors are parallel(dependent) to each other

1.2.4. Elimination matrix#

  • Use matrix to represent the elimination steps

\[ \begin{align*} E_{32}(E_{21}A) = (E_{32} \cdot E_{21})A = U \text{ (Associative law)} \end{align*} \]

  • \(E_{21}\) means elimination row 1 using row 2

Again, matrix * vector = the combination of the columns of the matrix, therefore, matrix * column = column, matrix * row = row.

1.2.5. Permutation matrix \(P\)#

  • Exchange the row

Exchange row 2 and row 1 \( \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \), example:

\[\begin{split} \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} c & d \\ a & b \end{bmatrix} \quad (\text{row operation}) \end{split}\]

Exchange column 2 and column 1, example:

\[\begin{split} \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} b & a \\ d & c \end{bmatrix} \quad (\text{column operation}) \end{split}\]

1.2.6. Inverse Matrix#

  • How we can reversing steps and transfer matrix from \(U \to A\)? (Inverse Matrix)

\[\begin{split} \begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{split}\]

  • \(\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\) means subtract \(3 \times \text{row1}\) from row2. If we want to reverse the operation, we just need to add \(3 \times \text{row1}\) to row2. That’s why we could easily calculate the inverse matrix.

1.2.7. Quiz#

Linear Algebra #2

  • Consider a linear equations

\[\begin{split} \begin{cases} 2x + 2y + 3z = 3 \\ x - y = 2 \\ -x + 2y + z = 1 \end{cases} \quad \cdots \cdots \cdots \text{(1)} \end{split}\]

  • Transform a matrix \( A = \begin{pmatrix} 2 & 2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{pmatrix} \) to an upper triangular matrix \( \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{pmatrix}.\)

\[\begin{split} \begin{bmatrix} 1 & 0 & 0 \\ -0.5 & 1 & 0 \\ -0.25 & 1.5 & 1 \end{bmatrix} \begin{bmatrix} 2 & 2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 2 & 3 \\ 0 & -2 & -\frac{3}{2} \\ 0 & 0 & \frac{1}{4} \end{bmatrix} \end{split}\]

1.3. Yalin Conclusion#

1.3.1. Row interpretation is suitable for first matrix, column interpretation is for second matrix [行前列后]#

  • \(E_{row operation}*A=U\)

  • \(A*E_{column operation} = U\)

1.4. The meaning of Matrix pre-multiplication(矩阵左乘)#

  1. \[\begin{split} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}, \end{split}\]

    we can get that, in a plane with basis \((1,0)\), \((0,1)\), the vector \((x_1, x_2)\) remains the same.

  2. According to this, we can say

    \[\begin{split} \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} \end{split}\]

    indicates, after changing the plane basis from \((1,0)\), \((0,1)\) to \((a_{11}, a_{21})\), \((a_{12}, a_{22})\), the coordinate of vector \((x_1, x_2)\) becomes \((b_1, b_2)\).

  3. Therefore, the matrix pre-multiplication is actually changing the basis.

Contents