Ctrl+K

Exploratory Data Analysis

9. Exploratory Data Analysis#

9.1. Basic Statistical Graphs#

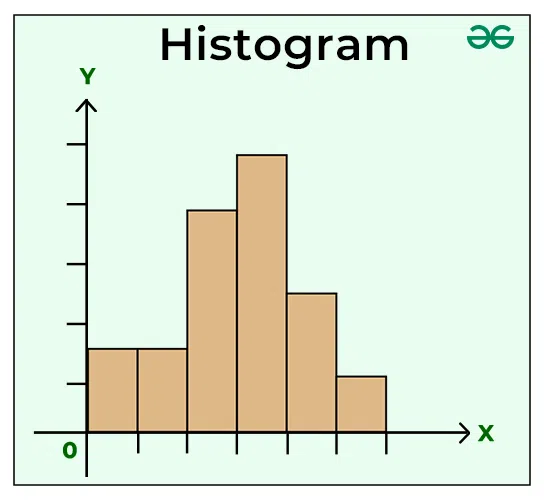
9.1.1. Univariate Distribution#

  1. Histogram

    • Bin / bandwidth

    img

  2. Box plot

    img

9.1.2. Bivariate Distribution#

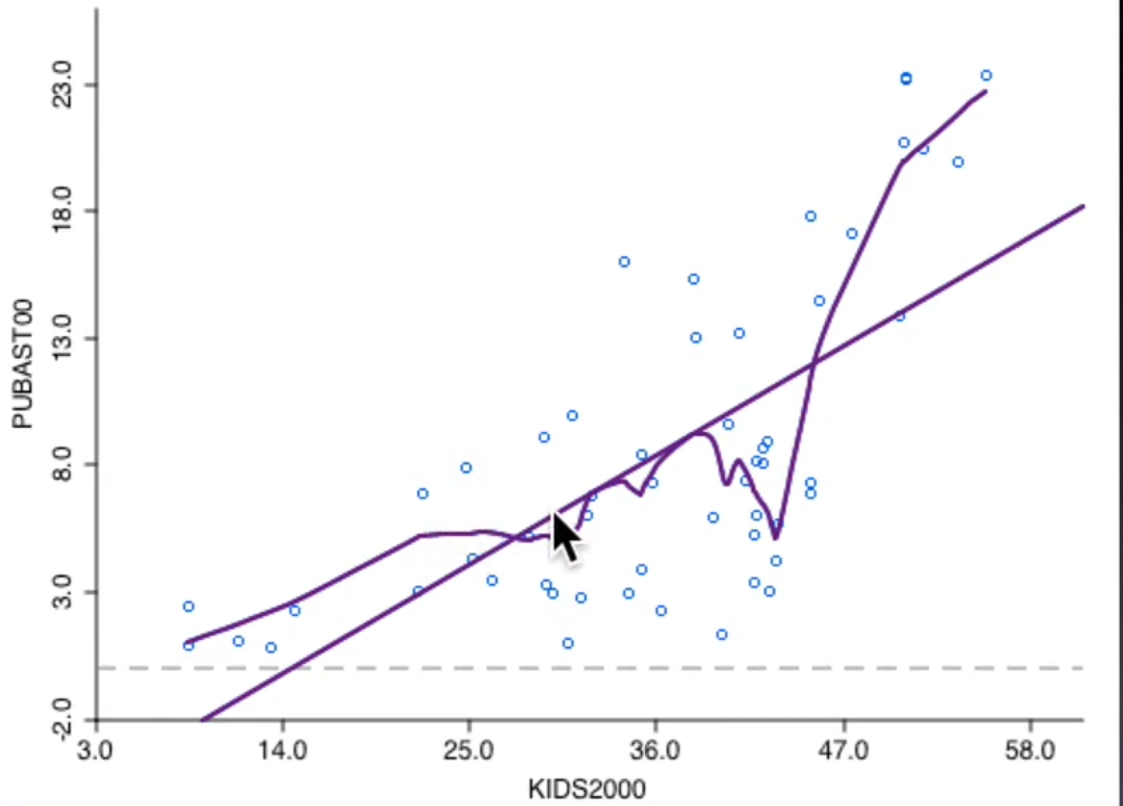
  1. Scatter plot

  2. Lowess Smoother

    • Local Regression

    • Slope based on a subset of observations

      1. For each \(x_i\),\(y_i\), fit based on (x,y) with x in neighborhood of \(x_i\)

    • Choice of bandwidth

      1. Short bandwidth yields spiky curve

      2. Wide bandwidth yields smoother curve

    img11

9.2. Spatial Heterogeneity#

  1. Structural breaks in the data with a spatial imprint

  2. Different distributions in different subregions a. Different mean, median

  3. Change in bivariate linear relationship

    • Structural beak in slope (Chow Test)

9.3. Tools for Spatial Heterogeneity Analysis (Bivariate)#

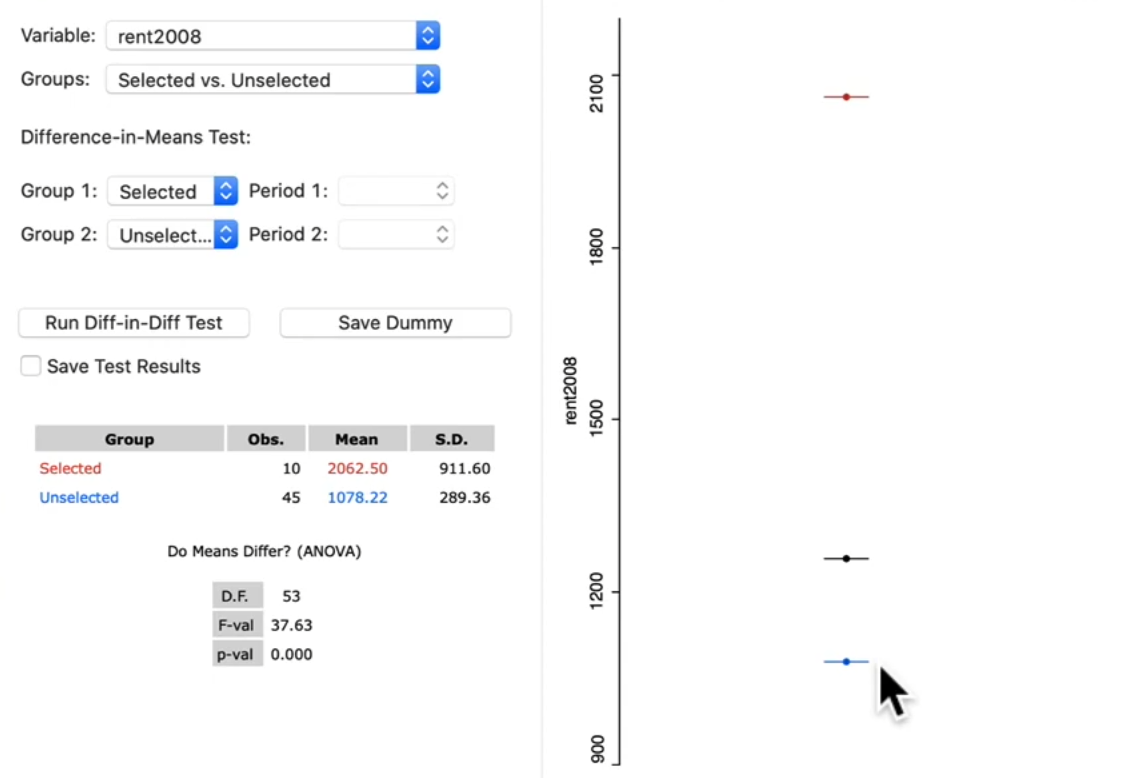
9.3.1. Averages Chart#

  1. Test on difference in mean

  2. Selected and Unselected

    • Spatial selection

  3. Test is F-statistic from dummy variable regression

    • Test the coefficient of dummy variable is significant or not

    image.png

9.3.2. Brushing the Scatter Plot#

  1. A brush is a selection shape

  2. Two slopes: selected and unselected

  3. As the brush moves, the slopes are recalculated in a dynamic way = dynamic brushing

  4. The matching observations in other windows are also selection

    • Dynamic brushing and linking

  5. Chow Test on Homogeneity of slopes

    • Hypothesis test on equality of slopes

      1. Overall regression slope

      2. Slope for selected

      3. Slope for unselected

  6. Link map brushing with Chow Test

    • Insight into spatial heterogeneity

    img14

9.4. Multivariate EDA#

9.4.1. Objective#

  1. Represent multi-dimensional data in two dimensions i. Dimension reduction ii. Projection

  2. Discover Structure, interaction, patterns

  3. Exploratory methods do not explain, it suggest hypotheses

9.5. Methods for multivariate EDA#

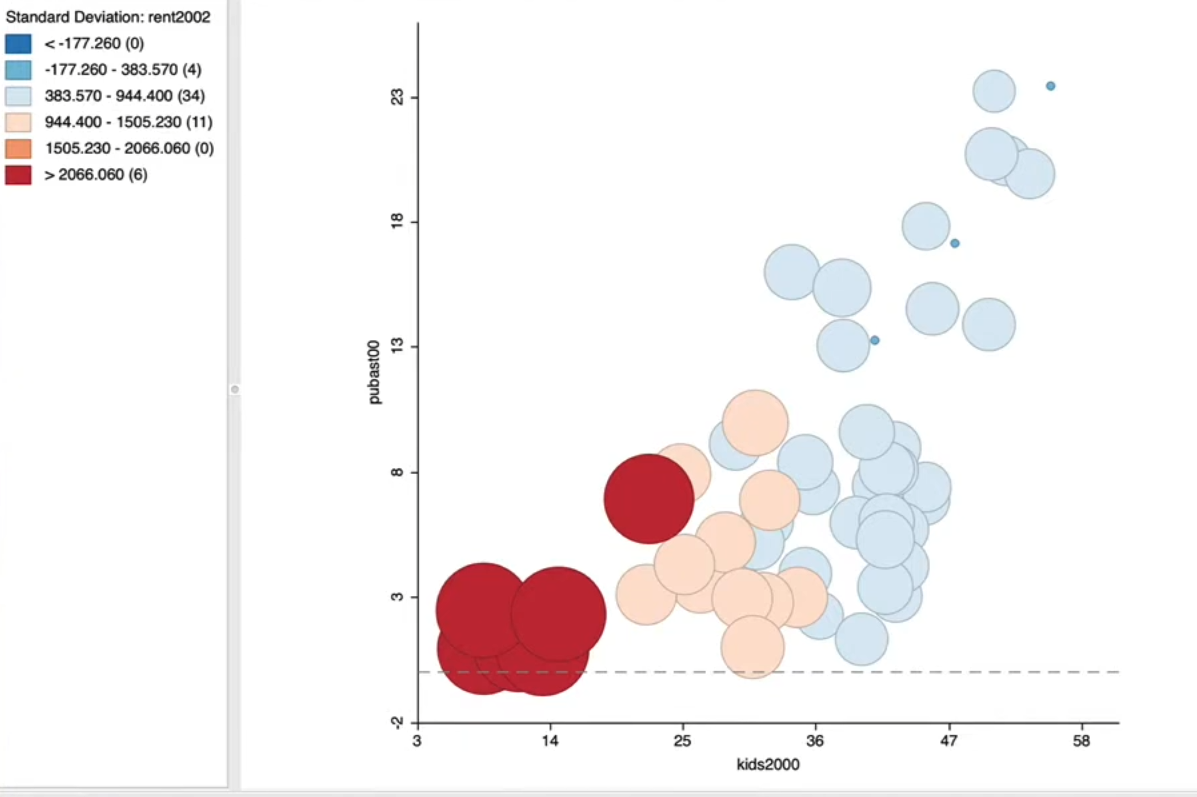
9.5.1. Bubble Chart#

  1. e.g. kids in family vs public assistants number vs high rent (sd)

  2. Enhanced Scatter Plot

    1. Size of bubble : third variable

    2. Color of bubble: Fourth variable

    3. Explore interaction among variables

    4. Explore structural breaks

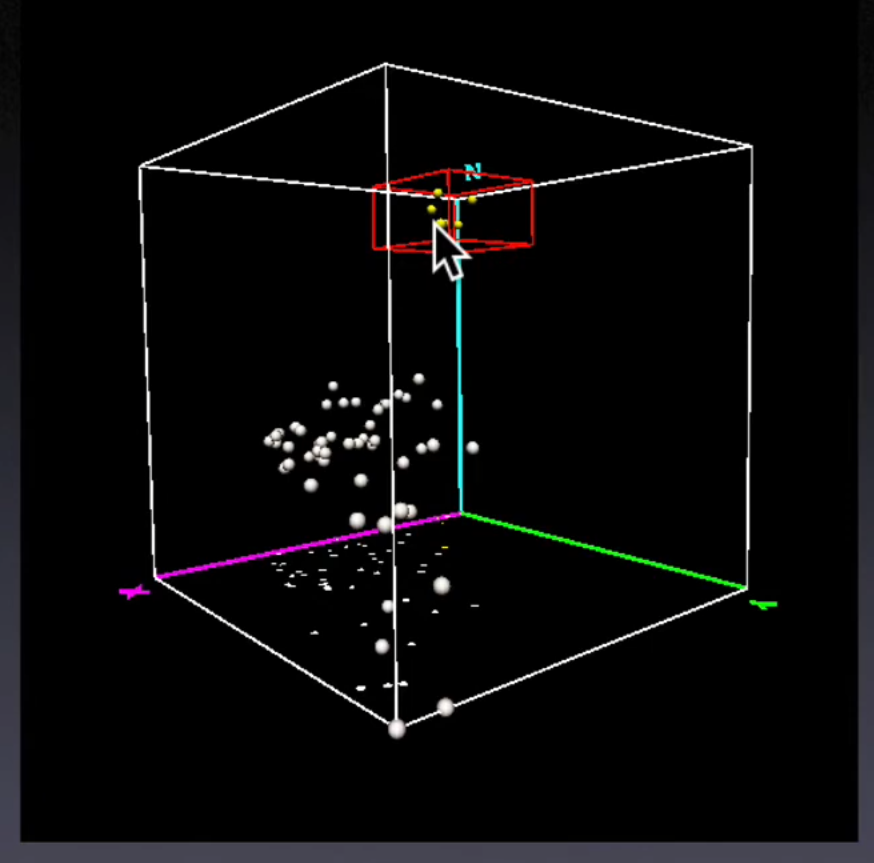
    image.png

9.5.2. 3D Scatter Plot#

  1. Points in a 3D data cube

  2. Two-Dimensional analysis on side panels

  3. Issues of perspective

    1. Zooming, Rotating

  4. Brushing the 3D data Cube

    image.png

9.5.3. Parallel coordinate plot(PCP)#

  1. Variables

    1. One parallel line for each variable

    2. Outliers are far from the main pack

  2. Observations

    1. A line connecting points on parallels

    2. The line is the counterpart of a point in the multidimensional data cube

    img

9.5.4. Conditional Plots#

  1. Interpretation of Conditional Plots

    1. Micro plots are similar, no effect of conditioning variables

    2. Micro plots are different, effect of conditioning variables

    image.png

Contents