11. Moran’s I and Geary’s C

11.1. Global Spatial Autocorrelation Measures

1. One statistic for the whole pattern

2. Test for clustering not for clusters (location)

11.1.1. Moran’s I (1948)

• The most commonly used for many spatial autocorrelation statistics

\[ \ I = \left[ \frac{\sum_i \sum_j W_{ij} \frac{z_i z_j}{S_0}}{\frac{\sum_i z_i^2}{N}} \right] = \frac{N \cdot \sum_i z_i \sum_j w_{ij} z_j}{s_0 \sum_i z_i^2} \]

• \(S_0 = \sum_i\sum_j W_{ij}\), \(Z_i = y_i-m_x\): deviations from mean

  • \(\sum_j w_{ij}z_j\) is the independent variable in this regression, called spatial lag

• Moran's I depends on spatial weights, relative magnitude for same weights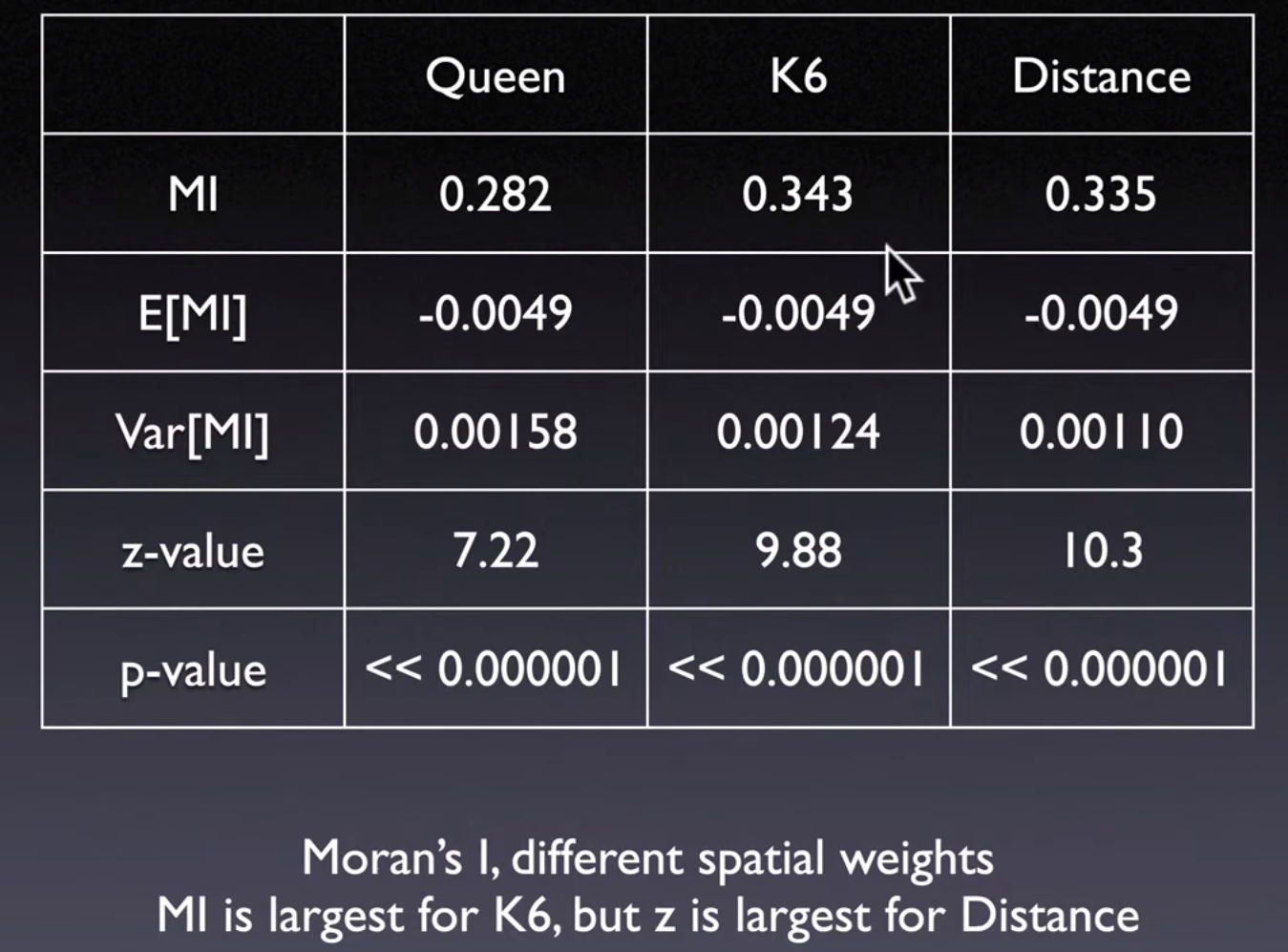

  

• Similar to Person Correlation, which is \((Cross Product)/Sd\), Here is autocorrelation,

11.1.2. Inference

1. How to assess whether the computed value of Moran's Index is significantly different from a value for a spatially random distribution

• Assume normal distribution

• Compare value to a reference distribution obtained from a series of randomly permuted patterns

  1. Positive and significant = clustering of like value

  2. Different Process can result in the same pattern

     1. True contagion: Evidence of clustering due to spatial interaction

        • Spatial interaction can through network other than geographical distance

     2. Apparent contagion: Evidence of clustering due to spatial heterogeneity

  3. Negative and significant = alternating values

2. Moran Z-value

\[ z = \frac{\text{Observed } I - \text{Mean}(I)}{sd} \]

• Z are comparable across variables and across spatial weights

  • Moran’s I are not comparable if spatial weight matrix are not same

  • Spatial weight matrix is for spatial similarity measuring

11.2. Geary’s C (1954)

1. Squared difference as measure of dissimilarity

   • Values between 0 and 2

2. Similar to notion of variogram (geo-statistics)

\[ C = \frac{(N - 1) \sum_i \sum_j w_{ij} (x_i - x_j)^2}{2s_0 \sum_i z_i^2} \]

• \(S_0 = \sum_i \sum_j W_{ij}\)

11.2.1. Interpretation

1. Positive spatial autocorrelation: \((c < 1)\) or \((z < 0)\)

2. Negative spatial autocorrelation: \((c > 1)\) or \((z > 0)\)

11.2.2. Inference

• Same to Moran's I