Ctrl+K

Spatial Autocorrelation

10. Spatial Autocorrelation#

10.1. Spatial Randomness#

10.1.1. The Null Hypothesis#

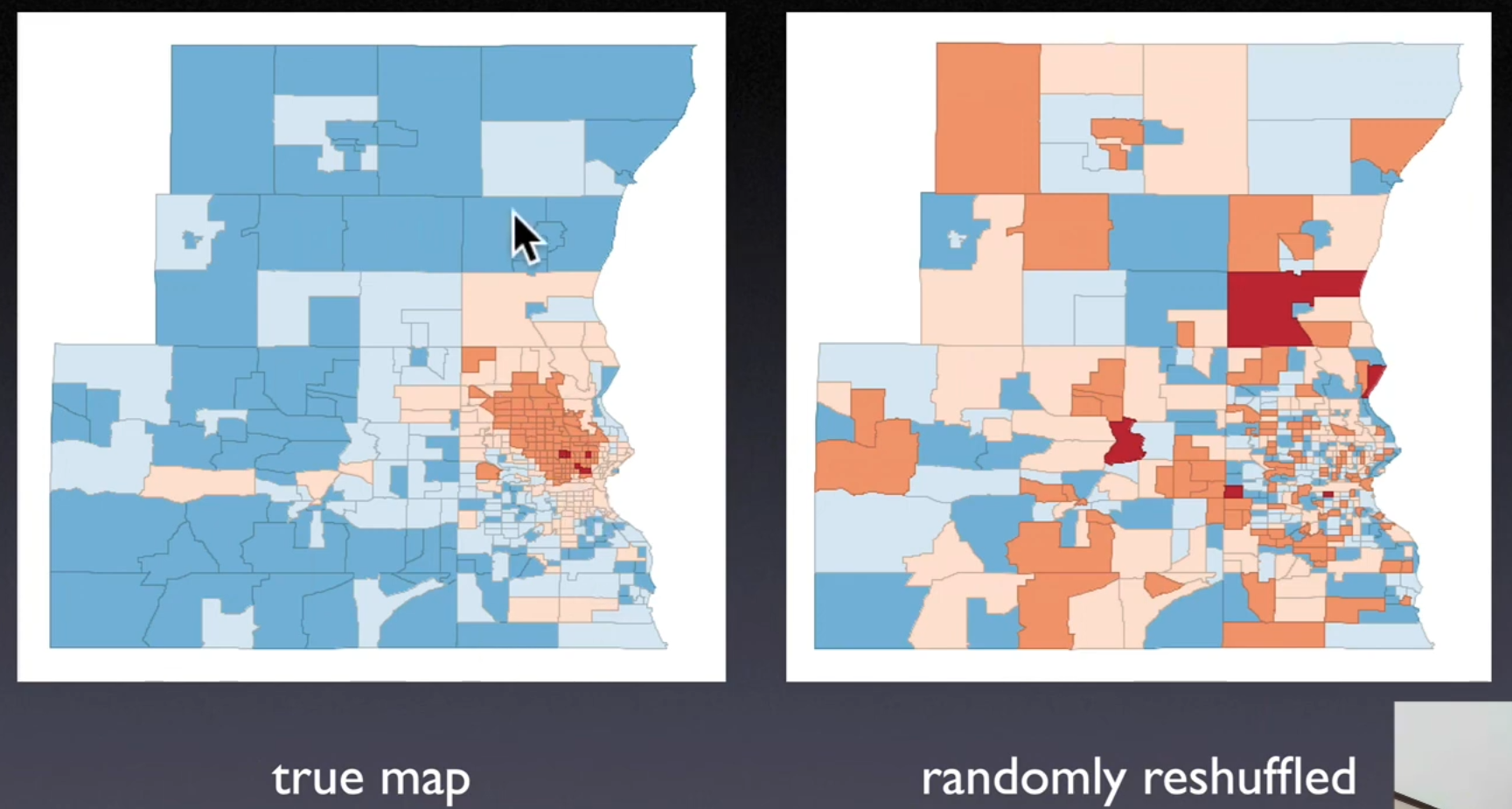
  1. Spatial randomness is absence of any pattern

  2. If rejected, then there is evidence of spatial structure

10.1.2. Interpreting Spatial Randomness#

  1. The observed spatial pattern of clues is equally likely as any other spatial pattern

    • Simultaneous view (Pattern)

  2. Value at one location does not depend on values at other (neighboring) locations

    • Conditional view

10.1.3. Operationalizing Spatial Randomness#

Random permutation or reshuffling of values Tobler's First Law of Geography

  1. Everything depends on everything else, but closer things more so

    1. Structures spatial dependence

    2. Importance of distance decay

      • Observations further apart are less correlate

      • Range of interaction - no spatial correlation beyond

image.png

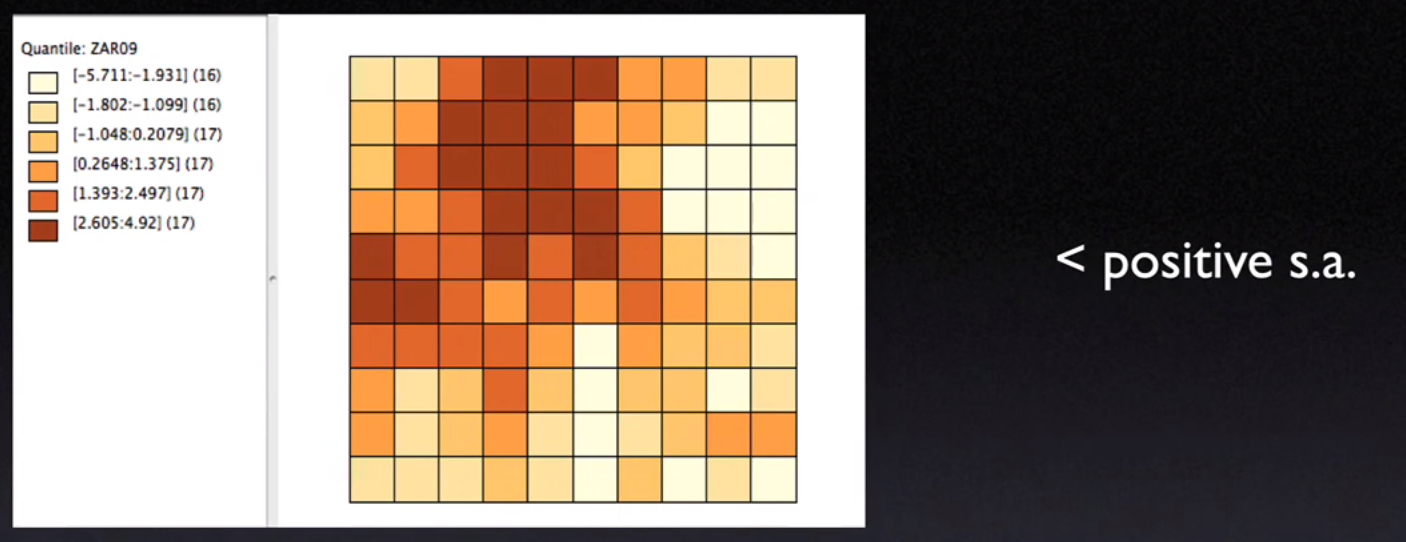
10.2. Positive and Negative spatial autocorrelation#

10.2.1. Positive Spatial Autocorrelation#

  1. Impression of clustering

  2. Clumps of like values

    • Like values can be either high (hot spots) or low (cold spots)

    img

10.2.2. Negative Spatial Autocorrelation#

  1. Checkerboard pattern

  2. Hard to distinguish from spatial randomness

    img

10.3. Spatial Autocorrelation Statistics#

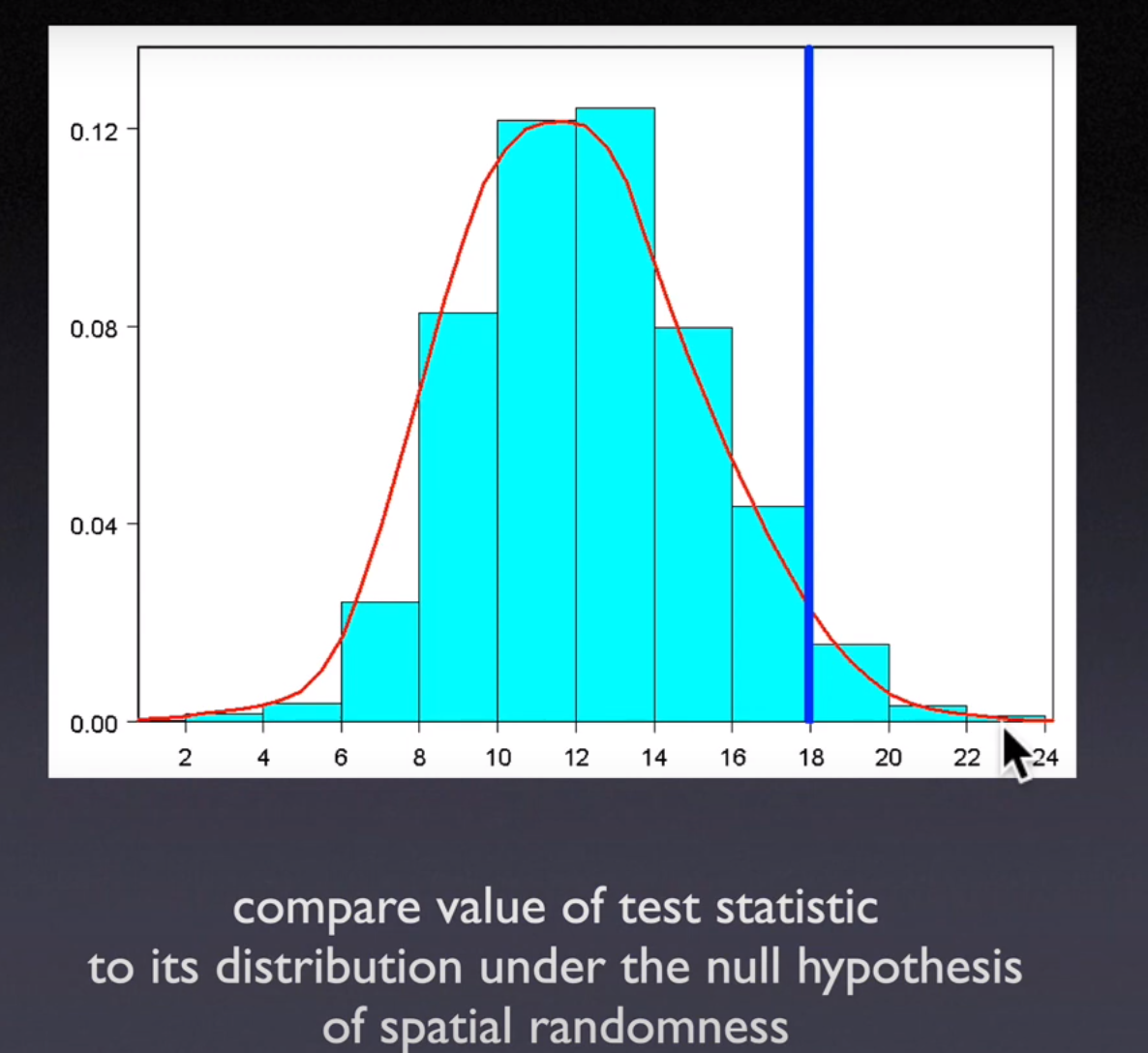
10.3.1. Test Statistics#

  1. Calculated from the data and compared to a reference distribution

  2. How likely is the value if it had occurred under null hypothesis (spatial randomness)

    • Type-one error: you reject the null hypothesis but it’s true

    • When unlikely (low p-value) the null hypothesis is rejected

image.png

10.4. Spatial Autocorrelation Statistic#

  • Captures both attribute similarity and locational similarity

  • Attribute Similarity

    1. Summary of similarity of observations for variable at different locations

    2. Construct \(f(y_i,y_j)\) at location \(i,j\)

10.4.1. Similarity Measure#

  • Cross product: \(y_i,y_j\)

  • Under randomness (null hypothesis), cross product is not systematically large or small, otherwise, suggests spatial patterns

10.4.2. Dissimilarity Measure#

  • Squared difference : \((y_i−y_j )^2\)

  • Absolute difference : \(|y_i−y_j |\)

10.4.3. Locational Similarity#

  • Formalizing the notion of neighbors \(=(W_ij)\), spatial weights

  • When are two Spatial units \(i\) and \(j\) a priori likely to interact

  • Not necessarily a geographical notion, can be based on social network or general distance concepts

10.5. General Form of Spatial Autocorrelation Statistic#

  1. Sum over all pairs of observations of the product of attribute similarity measure with a neighbor indicator (spatial weight)

    • \(\sum_{ij}f(x_i,x_j)W_{ij}\)

    • where \(f(x_i,x_j)\) is attribute similarity, \(W_ij\) is a spatial weight

Contents