Ctrl+K

Visualizing Spatial Autocorrelation

12. Visualizing Spatial Autocorrelation#

12.1. Moran Scatter Plot (Anselin 1996)#

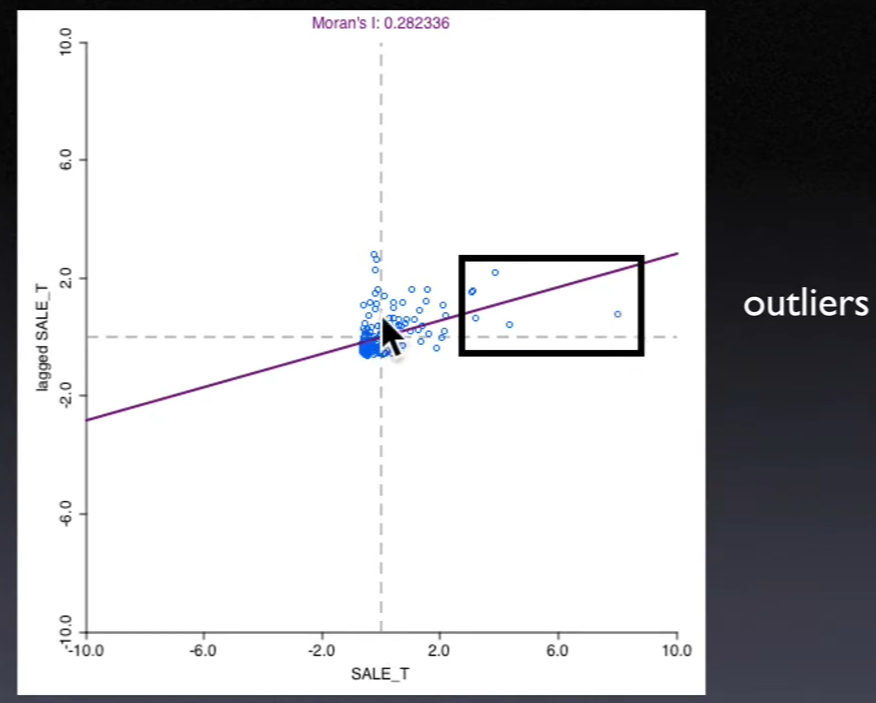
image.png

12.1.1. Interpretation#

Moran's I is slope in a regression of \(\sum_jw_{ij} z_j\) on \(z_i\)

  1. \(\sum_jw_{ij}z_j\) is the independent variable in this regression, called spatial lag

  2. The x-axis is value at each location, the y axis is spatial lag (weighted average of neighboring values)

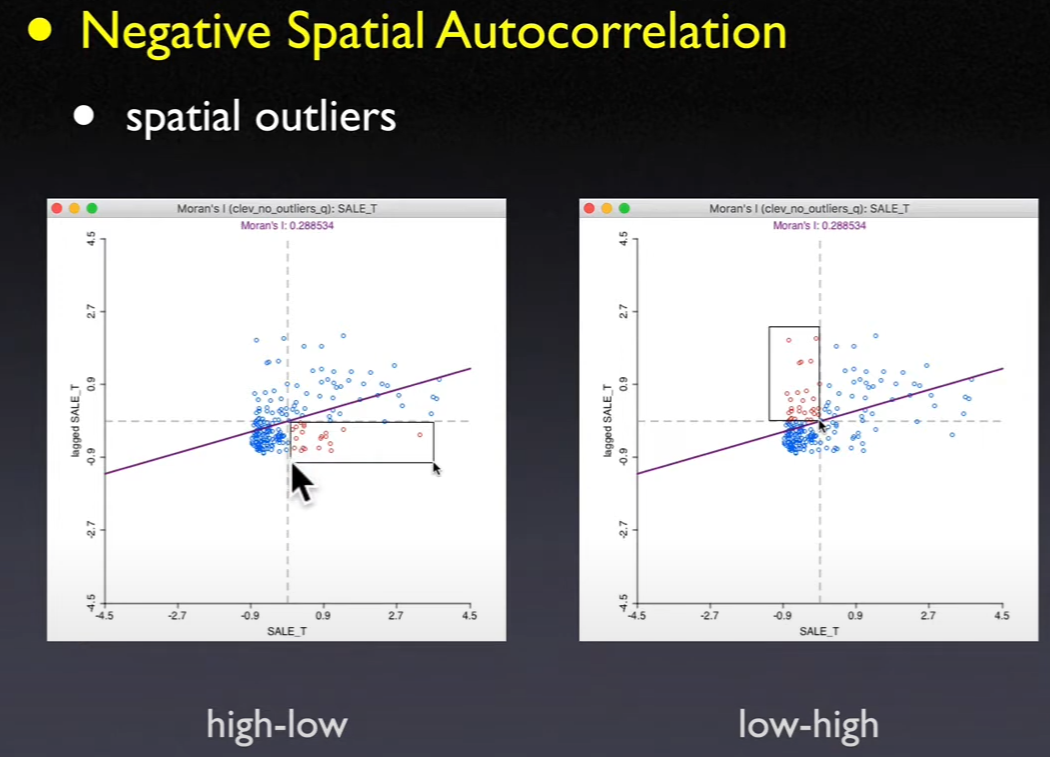
12.1.2. Categories of Local Spatial Autocorrelation#

  • Based on 4 quadrants / Relative to mean

  • Upper right and lower left are positive spatial autocorrelation

    • Clusters of like values

    • Locations are similar to their neighbors

  • Lower right and upper left are negative spatial autocorrelation

    • Spatial outliers

    • Locations are different from their neighbors

    img

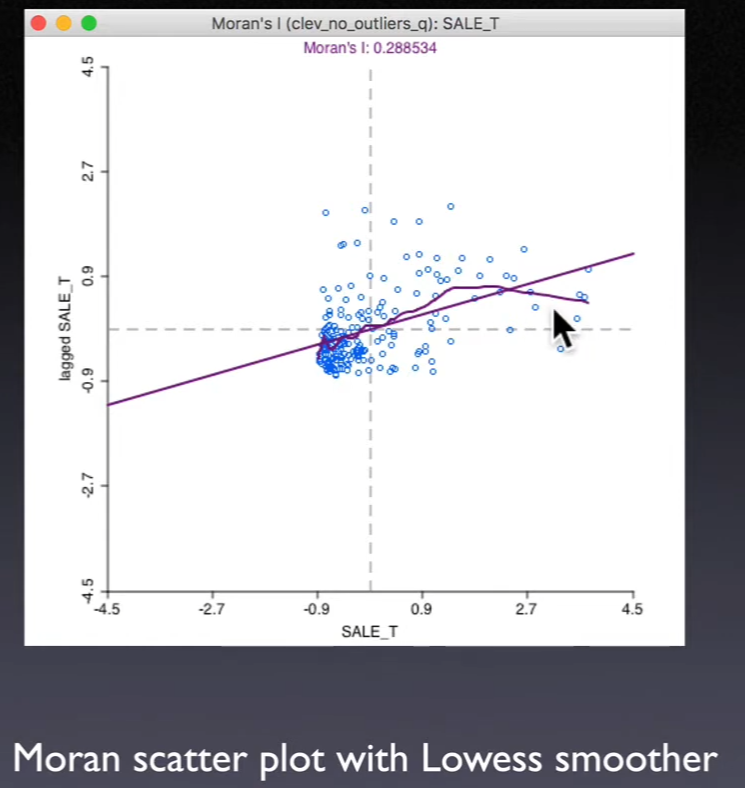
12.1.3. Smoothing the Moran Scatter Plot#

  1. Use local regression (LOWESS) as a nonlinear smoother

  2. Discover structural breaks in global spatial autocorrelation

    • Areas of high and low (or no) spatial autocorrelation

    • A form of spatial heterogeneity

    img

12.2. Correlogram#

12.2.1. Interpretation#

  1. Range of spatial autocorrelation (first hit the 0)

  2. Alternative to specifying spatial weights (data-driven)

  3. Sensitive to kernel fit (choose bandwidth and kernel function)

  4. May violate Tobler's law

img

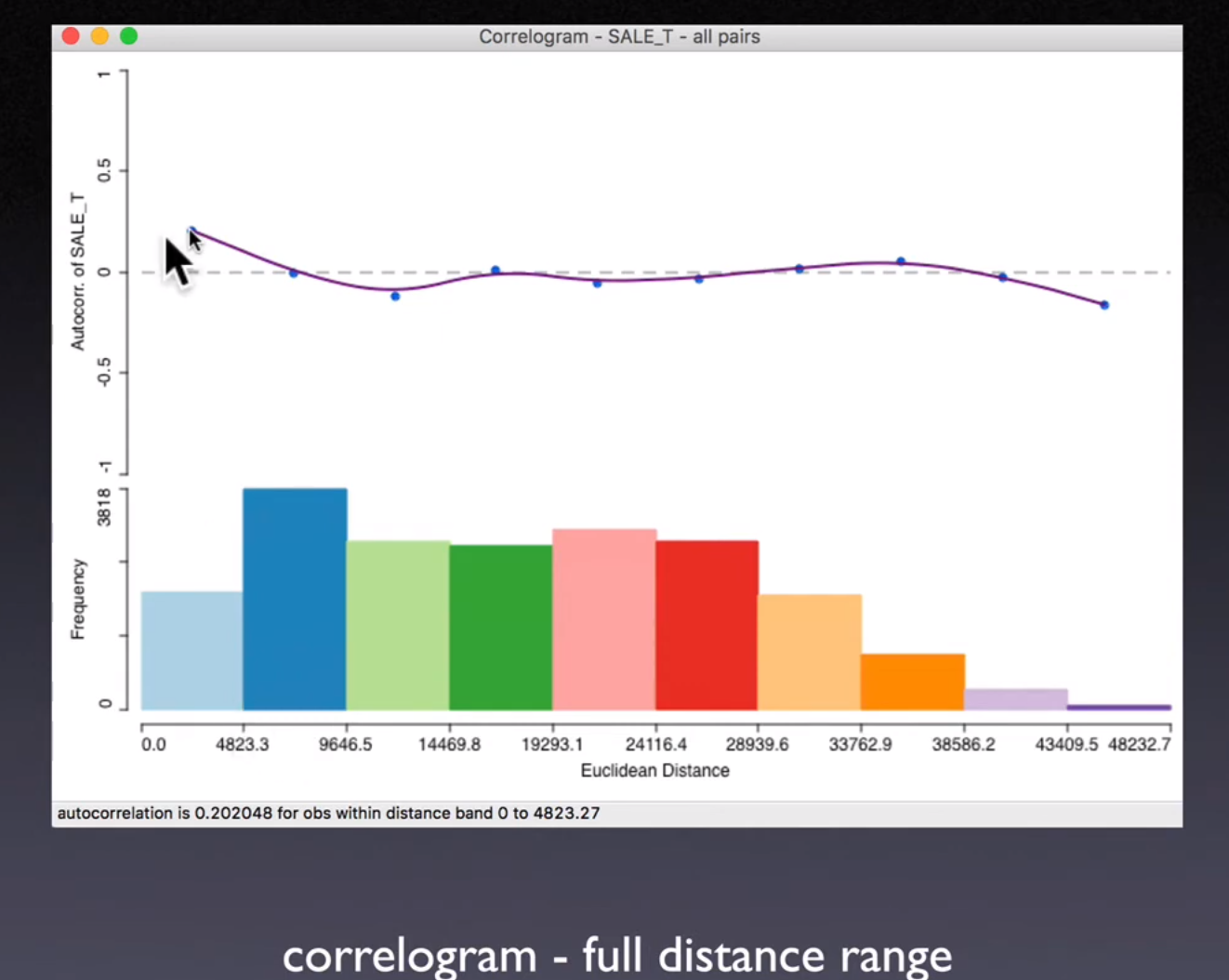
Moran's I plot is about Cross-product statistics of pair of observations, now we consider about non-parametric approach.

  1. Calculate the cross-product (covariance / auto-covariance) of each pair, and plot it across the distance

\[ \rho_{ij} = \rho(z_i, z_j) = \frac{\hat{z_i} * \hat{z_j}}{\frac{1}{n}\sum_n (z_n - z_m)^2} \]

  • \(\hat{Z_i}\): deviations from the mean

  • \(\frac{n(n-1)}{2}\) individual values of \(\rho_{ij}\) (unique pair from \(n\) elements)

  1. Fit the function of \(\rho*{ij} = g(d*{ij})\)

    • Use kernel estimator / local regression

      • Depends on choice of kernel function and bandwidth

      • Values of the estimated \(g(d\_{ij})\) do not necessarily result in a valid variance-covariance matrix

    • When first hit 0, means how far the spatial interaction goes, the following is waving around 0, basically the noise

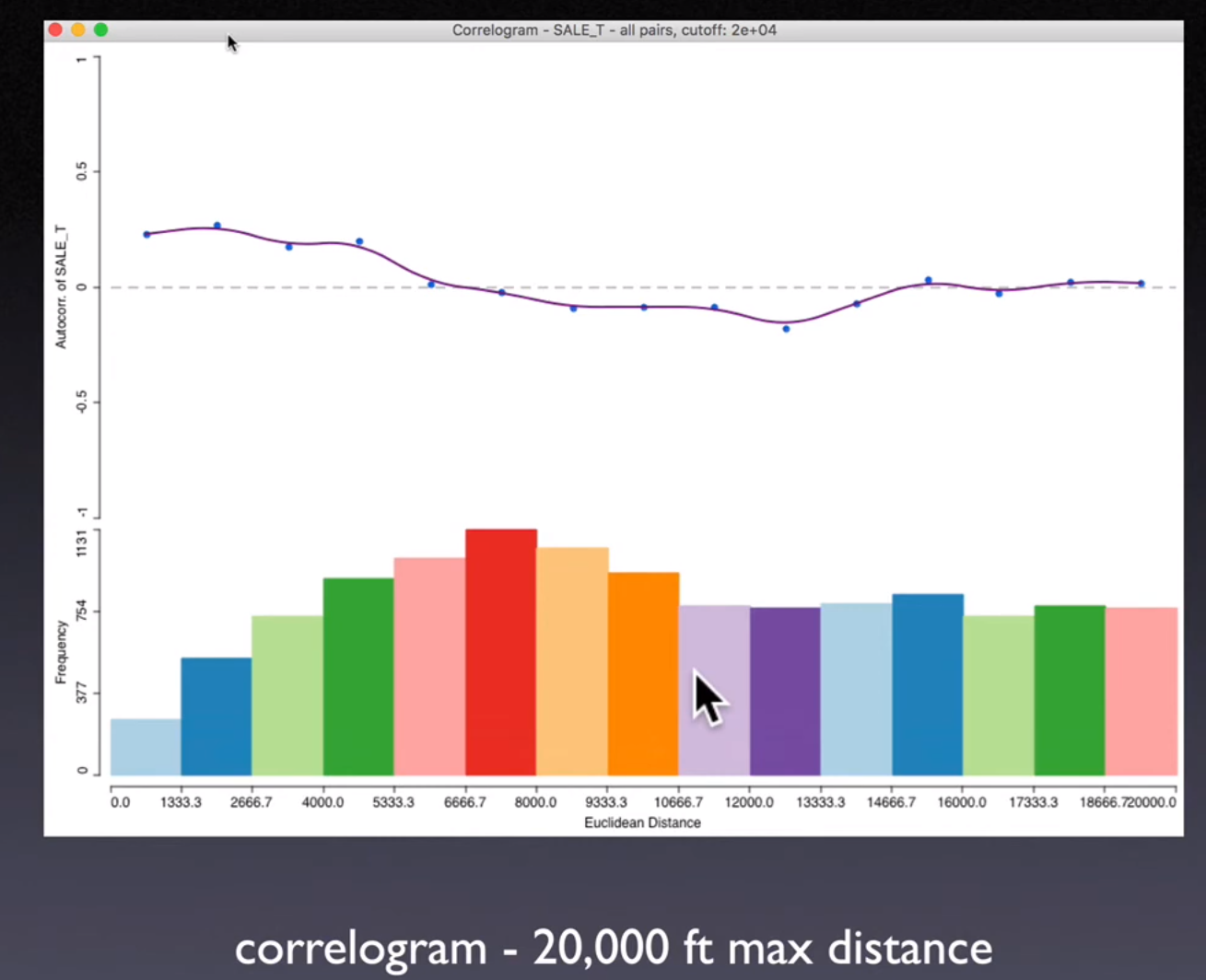
  2. Problems

    • When distance goes larger, the pair of observations decrease rapidly.

    • These “high-leverage” points may distort the whole pattern

    • Solution: Cut-off the distance by certain point

    img

12.3. Smoothed Distance Scatter Plot (Anselin and Li, 2020)#

Plot geographical distance on the x-axis, and attribute distance on the y-axis

  • Euclidean geographical distance

\[ d_{ij} = \left[ (x_i - x_j)^2 + (y_i - y_j)^2 \right]^{1/2} \]

  • Euclidean distance in attribute space

\[ v_{ij} = \left[ \sum_k (z_{ki} - z_{kj})^2 \right]^{1/2} \]

12.3.1. Concern#

  1. Too many points \(\left( \frac{n(n-1)}{2} \right)\)

    • Smooth the scatter plot

  2. Tobler’s law i. Attribute distance should increase with geographical distance

  3. We can also calculate the attribute distance of multiple variables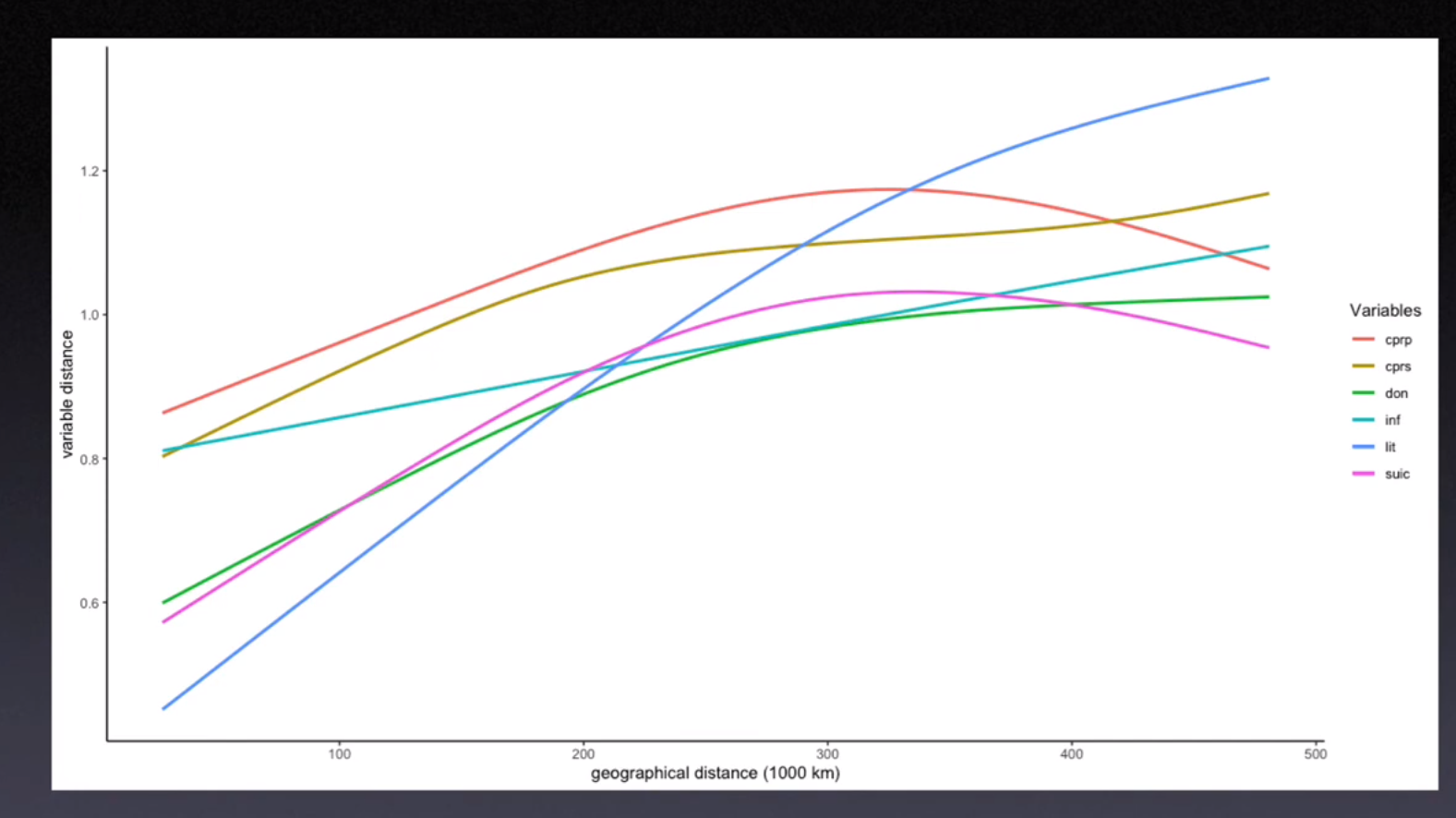

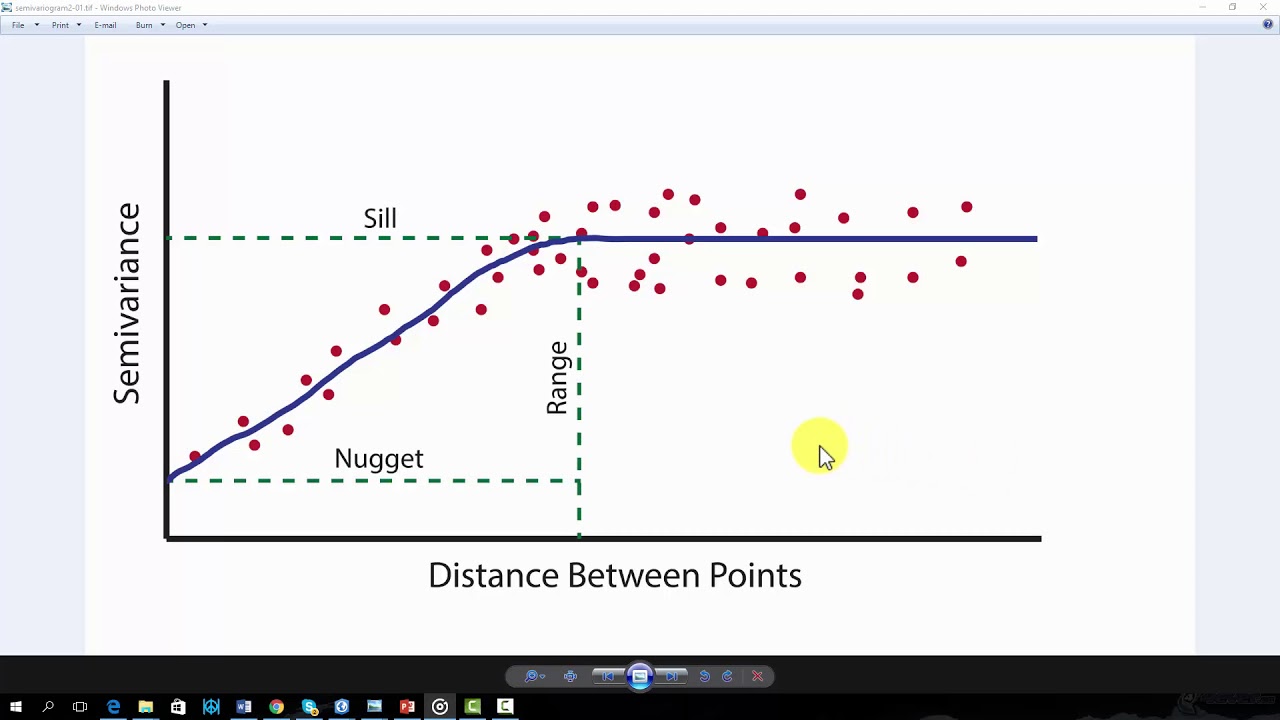
    img

12.4. Semi-variogram (Matheron, 1963)#

12.4.1. Definition#

  1. Semi-variance \(\gamma(s_1, s_2)\) is half the average squared difference between the value at points \(s_1\) and \(s_2\), it’s defined as

\[ \gamma(s_1, s_2) = \frac{\sum_v (s_1 - s_2)^2}{2V} \]

  1. Fit the function \(\rho(s*1, s_2) = g(h)\)

    • \(h\) represents the geographical distance

    • The exponential variogram model

\[ \gamma(h) = (s - n)(1 - \exp(-h/(ra))) + n1*{(0, \infty)}(h) \]

  • The spherical variogram model

\[ \gamma(h) = (s - n)\left(\left(\frac{3h}{2r} - \frac{h^3}{2r^3}\right)1*{(0, r)}(h) + 1*{[r, \infty)}(h)\right) + n1*{(0, \infty)}(h) \]

  • The Gaussian variogram model

\[ \gamma(h) = (s - n)\left(1 - \exp\left(-\frac{h^2}{r^2a}\right)\right) + n1_{(0, \infty)}(h) \]

12.4.2. Interpretation#

  • Nugget \(n\): Due to the measurement error or spatial source variation of smaller distance than sample unit, the value at the same location might have a different value as well.

  • Sill \(s\): Limit of the variogram tending to infinity lag distances.

  • Range \(r\): The distance in which the difference of the variogram from the sill becomes negligible. indicates the range of spatial autocorrelation

    img

Contents