10. Tensor#
10.1. What’s in a tensor?#
Tensors are “just” multi-dimensional arrays optimized for fast computation
Technically, a
tensorfeels a lot like anR6object, in that you can access its fields and methods using$-syntax.
t1 <- torch_tensor(1)
t1
## torch_tensor
## 1
## [ CPUFloatType{1} ]
This is a tensor that holds just a single value, 1. * It “lives” on the
CPU, and its type is Float * {1} indicates the tensor shape
instead of the stored value. Here, we have a one-dimensional
tensor, that is, a vector. * We can use the aforementioned
$-syntax to individually ascertain these properties
t1$dtype
## torch_Float
t1$device
## torch_device(type='cpu')
t1$shape
## [1] 1
We can also directly change some of these properties, making use of the
tensor object’s $to() method:
t2 <- t1$to(dtype = torch_int())
t2$dtype
## torch_Int
# only applicable if you have a GPU
t2 <- t1$to(device = "cuda")
t2$device
## torch_device(type='cuda', index=0)
Change it’s shape
t3 <- t1$view(c(1, 1))
t3$shape
## [1] 1 1
Conceptually, this is analogous to a one-element vector as well as a
one-element matrix:
c(1)
## [1] 1
matrix(1)
## [,1]
## [1,] 1
10.2. Creating tensors#
calling torch_tensor() and passing in an R value.
t3 <- torch_tensor(c(1,2,3))
t3
## torch_tensor
## 1
## 2
## 3
## [ CPUFloatType{3} ]
t4 <- torch_tensor(matrix(data= c(1,1,2,2),ncol = 2))
t4
## torch_tensor
## 1 2
## 1 2
## [ CPUFloatType{2,2} ]
10.2.1. Tensors from values#
Above, we passed in a one-element vector to torch_tensor(); we can pass in longer vectors just the same way
torch_tensor(1:5)
## torch_tensor
## 1
## 2
## 3
## 4
## 5
## [ CPULongType{5} ]
torchdetermines a suitabledata typeitselfHere, the assumption is that an integer type is desired, and torch chooses the highest-precision type available (
torch_long()is synonymous totorch_int64()).If we want a floating-point tensor instead, we can use
$to()on the newly created instance (as we saw above).
Alternatively, we can just let
torch_tensor()know right away:
torch_tensor(1:5, dtype = torch_float())
## torch_tensor
## 1
## 2
## 3
## 4
## 5
## [ CPUFloatType{5} ]
Analogously, the default device is the CPU; but we can also create a
tensor that, right from the outset, is located on the GPU:
torch_tensor(1:5, device = "cuda")
## torch_tensor
## 1
## 2
## 3
## 4
## 5
## [ CUDALongType{5} ]
We can pass in an R matrix just the same way:
torch_tensor(matrix(1:9, ncol = 3))
## torch_tensor
## 1 4 7
## 2 5 8
## 3 6 9
## [ CPULongType{3,3} ]
torch_tensor(matrix(1:9, ncol = 3, byrow = TRUE))
## torch_tensor
## 1 2 3
## 4 5 6
## 7 8 9
## [ CPULongType{3,3} ]
What about higher-dimensional data? Following the same principle, we can
pass in an array:
torch_tensor(array(1:24, dim = c(4, 3, 2)))
## torch_tensor
## (1,.,.) =
## 1 13
## 5 17
## 9 21
##
## (2,.,.) =
## 2 14
## 6 18
## 10 22
##
## (3,.,.) =
## 3 15
## 7 19
## 11 23
##
## (4,.,.) =
## 4 16
## 8 20
## 12 24
## [ CPULongType{4,3,2} ]
Here, pictorially, is the object we created (fig. 3.1). Let’s call the axis that extends to the right x, the one that goes into the page, y, and the one that points up, z. Then the tensor extends 4, 3, and 2 units, respectively, in the x, y, and z directions.

Example for 3 * 2 * 5 tensor
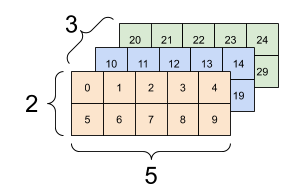
Compare that with how the tensor prints, above. Array and tensor
slice the object in different ways. * The tensor slices its values
into 3x2 rectangles, extending up and to the back, one for each of the
four x-values. * The array, on the other hand, splits them up by
z-value, resulting in two big 4x3 slices that go up and to the right.
array(1:24, dim = c(4, 3, 2))
## , , 1
##
## [,1] [,2] [,3]
## [1,] 1 5 9
## [2,] 2 6 10
## [3,] 3 7 11
## [4,] 4 8 12
##
## , , 2
##
## [,1] [,2] [,3]
## [1,] 13 17 21
## [2,] 14 18 22
## [3,] 15 19 23
## [4,] 16 20 24
10.2.2. Tensors from specifications#
There are two broad conditions when torch’s bulk creation functions
will come in handy 1. when you don’t care about individual tensor
values, but only about their distribution. 2. They follow some
conventional pattern.
When we use bulk creation functions, instead of individual values we
specify the shape they should have. * Here, for example, we
instantiate a 3x3 tensor, populated with standard-normally
distributed values:
torch_randn(3, 3)
## torch_tensor
## 1.0917 0.2943 -1.2244
## 0.8632 1.0131 -0.8944
## 0.1360 -1.2286 -0.9151
## [ CPUFloatType{3,3} ]
And here is the equivalent for values that are uniformly distributed between zero and one:
torch_rand(3, 3)
## torch_tensor
## 0.9881 0.8841 0.4892
## 0.8545 0.3124 0.4425
## 0.0556 0.1737 0.2220
## [ CPUFloatType{3,3} ]
Often, we require tensors of all ones, or all zeroes:
torch_zeros(2, 5)
## torch_tensor
## 0 0 0 0 0
## 0 0 0 0 0
## [ CPUFloatType{2,5} ]
torch_ones(2, 2)
## torch_tensor
## 1 1
## 1 1
## [ CPUFloatType{2,2} ]
let’s see how to create some matrix types that are common in linear algebra. 1. Here’s an identity matrix:
torch_eye(n = 5)
## torch_tensor
## 1 0 0 0 0
## 0 1 0 0 0
## 0 0 1 0 0
## 0 0 0 1 0
## 0 0 0 0 1
## [ CPUFloatType{5,5} ]
Here, a diagonal matrix:
torch_diag(c(1, 2, 3))
## torch_tensor
## 1 0 0
## 0 2 0
## 0 0 3
## [ CPUFloatType{3,3} ]
10.2.3. Tensors from datasets#
First, let’s try JohnsonJohnson that comes with base R. * It is a
time series of quarterly earnings per Johnson & Johnson share.
JohnsonJohnson
## Qtr1 Qtr2 Qtr3 Qtr4
## 1960 0.71 0.63 0.85 0.44
## 1961 0.61 0.69 0.92 0.55
## 1962 0.72 0.77 0.92 0.60
## 1963 0.83 0.80 1.00 0.77
## 1964 0.92 1.00 1.24 1.00
## 1965 1.16 1.30 1.45 1.25
## 1966 1.26 1.38 1.86 1.56
## 1967 1.53 1.59 1.83 1.86
## 1968 1.53 2.07 2.34 2.25
## 1969 2.16 2.43 2.70 2.25
## 1970 2.79 3.42 3.69 3.60
## 1971 3.60 4.32 4.32 4.05
## 1972 4.86 5.04 5.04 4.41
## 1973 5.58 5.85 6.57 5.31
## 1974 6.03 6.39 6.93 5.85
## 1975 6.93 7.74 7.83 6.12
## 1976 7.74 8.91 8.28 6.84
## 1977 9.54 10.26 9.54 8.73
## 1978 11.88 12.06 12.15 8.91
## 1979 14.04 12.96 14.85 9.99
## 1980 16.20 14.67 16.02 11.61
If we just pass it directly to torch_tensor(), we will get a vector,
similar to unclass(JohnsonJohnson)
torch_tensor(JohnsonJohnson)
## torch_tensor
## 0.7100
## 0.6300
## 0.8500
## 0.4400
## 0.6100
## 0.6900
## 0.9200
## 0.5500
## 0.7200
## 0.7700
## 0.9200
## 0.6000
## 0.8300
## 0.8000
## 1.0000
## 0.7700
## 0.9200
## 1.0000
## 1.2400
## 1.0000
## 1.1600
## 1.3000
## 1.4500
## 1.2500
## 1.2600
## 1.3800
## 1.8600
## 1.5600
## 1.5300
## 1.5900
## ... [the output was truncated (use n=-1 to disable)]
## [ CPUFloatType{84} ]
torch can only work with what it is given; and here, what it is given
is actually a vector of doubles arranged in quarterly order. The
data just print the way they do because they are of class ts:
unclass(JohnsonJohnson)
## [1] 0.71 0.63 0.85 0.44 0.61 0.69 0.92 0.55 0.72 0.77 0.92 0.60
## [13] 0.83 0.80 1.00 0.77 0.92 1.00 1.24 1.00 1.16 1.30 1.45 1.25
## [25] 1.26 1.38 1.86 1.56 1.53 1.59 1.83 1.86 1.53 2.07 2.34 2.25
## [37] 2.16 2.43 2.70 2.25 2.79 3.42 3.69 3.60 3.60 4.32 4.32 4.05
## [49] 4.86 5.04 5.04 4.41 5.58 5.85 6.57 5.31 6.03 6.39 6.93 5.85
## [61] 6.93 7.74 7.83 6.12 7.74 8.91 8.28 6.84 9.54 10.26 9.54 8.73
## [73] 11.88 12.06 12.15 8.91 14.04 12.96 14.85 9.99 16.20 14.67 16.02 11.61
## attr(,"tsp")
## [1] 1960.00 1980.75 4.00
10.3. Operations on tensors#
We can perform all the usual mathematical operations on tensors.: add,
subtract, divide …
These operations are available as functions (starting with
torch_) as well as as methods on objects (invoked with$-syntax).
t1 <- torch_tensor(c(1, 2))
t2 <- torch_tensor(c(3, 4))
torch_add(t1, t2)
## torch_tensor
## 4
## 6
## [ CPUFloatType{2} ]
# equivalently
t1$add(t2)
## torch_tensor
## 4
## 6
## [ CPUFloatType{2} ]
In both cases, a new object is created; neither t1 nor t2 are
modified. There exists an alternate method that modifies its object
in-place:
t1
## torch_tensor
## 1
## 2
## [ CPUFloatType{2} ]
t1$add_(t2)
## torch_tensor
## 4
## 6
## [ CPUFloatType{2} ]
t1
## torch_tensor
## 4
## 6
## [ CPUFloatType{2} ]
In fact, the same pattern applies for other operations: Whenever you see an underscore appended, the object is modified in-place.
Let’s start with the dot product of two one-dimensional structures,
i.e., vectors.
t1 <- torch_tensor(1:3)
t2 <- torch_tensor(4:6)
t1$dot(t2)
## torch_tensor
## 32
## [ CPULongType{} ]
torchdoes not distinguish betweenrow vectorsandcolumn vectors.if we multiply a
vectorwith amatrix, usingtorch_matmul(), we don’t need to worry about the vector’s orientation either:
t3 <- torch_tensor(matrix(1:12, ncol = 3, byrow = TRUE))
t3$matmul(t1)
## torch_tensor
## 14
## 32
## 50
## 68
## [ CPULongType{4} ]
The same function, torch_matmul(), would be used to multiply two
matrices. Note how this is different from what torch_multiply() does,
namely, scalar-multiply its arguments:
t1 <- torch_tensor(1:3)
t2 <- torch_tensor(4:6)
torch_multiply(t1, t2)
## torch_tensor
## 4
## 10
## 18
## [ CPULongType{3} ]
10.3.1. Summary operations#
m <- outer(1:3, 1:6)
m
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1 2 3 4 5 6
## [2,] 2 4 6 8 10 12
## [3,] 3 6 9 12 15 18
sum(m)
## [1] 126
apply(m, 1, sum)
## [1] 21 42 63
apply(m, 2, sum)
## [1] 6 12 18 24 30 36
And now, the torch equivalents. We start with the overall sum.
t <- torch_outer(torch_tensor(1:3), torch_tensor(1:6))
t$sum()
## torch_tensor
## 126
## [ CPULongType{} ]
It gets more interesting for the row and column sums. The dim argument
tells torch which dimension(s) to sum over. Passing in dim = 1, we
see:
t$sum(dim = 1)
## torch_tensor
## 6
## 12
## 18
## 24
## 30
## 36
## [ CPULongType{6} ]
Unexpectedly, these are the column sums! Before drawing conclusions,
let’s check what happens with dim = 2:
t$sum(dim = 2)
## torch_tensor
## 21
## 42
## 63
## [ CPULongType{3} ]
Instead, the conceptual difference is specific to aggregating, or
grouping, operations. In R, grouping, in fact, nicely characterizes
what we have in mind: We group by row (dimension 1) for row summaries,
by column (dimension 2) for column summaries. In torch, the thinking is
different: We collapse the columns (dimension 2) to compute row
summaries, the rows (dimension 1) for column summaries.
The same thinking applies in higher dimensions. Assume, for example, that we been recording time series data for four individuals. There are two features, and both of them have been measured at three times. If we were planning to train a recurrent neural network (much more on that later), we would arrange the measurements like so:
Dimension 1: Runs over individuals.
Dimension 2: Runs over points in time.
Dimension 3: Runs over features.
The tensor then would look like this:
t <- torch_randn(4, 3, 2)
t
## torch_tensor
## (1,.,.) =
## 1.4176 0.6129
## -0.7762 -0.2163
## -0.1870 0.0977
##
## (2,.,.) =
## -0.0486 -1.6754
## -0.7790 -1.4072
## 1.7094 0.6100
##
## (3,.,.) =
## -0.6665 0.7684
## 0.0685 0.2067
## 0.9274 0.3285
##
## (4,.,.) =
## -2.5222 -0.6573
## -0.1464 0.1550
## 0.9306 -0.3727
## [ CPUFloatType{4,3,2} ]
To obtain feature averages, independently of subject and time, we would collapse dimensions 1 and 2:
t$mean(dim = c(1, 2))
## torch_tensor
## 0.001 *
## -6.0413
## -129.1528
## [ CPUFloatType{2} ]
If, on the other hand, we wanted feature averages, but individually per person, we’d do:
t$mean(dim = 2)
## torch_tensor
## 0.1515 0.1648
## 0.2939 -0.8242
## 0.1098 0.4345
## -0.5793 -0.2917
## [ CPUFloatType{4,2} ]
10.4. Accessing parts of a tensor#
10.4.1. Indexing and Slicing#
In the below example, we ask for the first column of a two-dimensional
tensor; the result is one-dimensional, i.e., a vector:
t <- torch_tensor(matrix(1:9, ncol = 3, byrow = TRUE))
t
## torch_tensor
## 1 2 3
## 4 5 6
## 7 8 9
## [ CPULongType{3,3} ]
t[1, ]
## torch_tensor
## 1
## 2
## 3
## [ CPULongType{3} ]
If we specify drop = FALSE, though, dimensionality is preserved:
t[1, , drop = FALSE]
## torch_tensor
## 1 2 3
## [ CPULongType{1,3} ]
When slicing, there are no singleton dimensions – and thus, no
additional considerations to be taken into account:
t <- torch_rand(3, 3, 3)
t
## torch_tensor
## (1,.,.) =
## 0.3448 0.2467 0.2844
## 0.0130 0.0119 0.4501
## 0.4605 0.1153 0.9454
##
## (2,.,.) =
## 0.6728 0.4534 0.6797
## 0.5317 0.6467 0.8967
## 0.1564 0.0813 0.7384
##
## (3,.,.) =
## 0.0476 0.1795 0.0142
## 0.8283 0.2712 0.2839
## 0.3849 0.6851 0.2013
## [ CPUFloatType{3,3,3} ]
t[1:2, 2:3, c(1, 3)]
## torch_tensor
## (1,.,.) =
## 0.0130 0.4501
## 0.4605 0.9454
##
## (2,.,.) =
## 0.5317 0.8967
## 0.1564 0.7384
## [ CPUFloatType{2,2,2} ]
10.4.2. Advanced query#
One of these extensions concerns accessing the last element in a
tensor. Conveniently, in torch, we can use -1 to accomplish that:
t <- torch_tensor(matrix(1:4, ncol = 2, byrow = TRUE))
t
## torch_tensor
## 1 2
## 3 4
## [ CPULongType{2,2} ]
t[-1, -1]
## torch_tensor
## 4
## [ CPULongType{} ]
Another useful feature extends slicing syntax to allow for a step
pattern, to be specified after a second colon. Here, we request values
from every second column between columns one and eight:
t <- torch_tensor(matrix(1:20, ncol = 10, byrow = TRUE))
t
## torch_tensor
## 1 2 3 4 5 6 7 8 9 10
## 11 12 13 14 15 16 17 18 19 20
## [ CPULongType{2,10} ]
t[ , 1:8:2]
## torch_tensor
## 1 3 5 7
## 11 13 15 17
## [ CPULongType{2,4} ]
Finally, sometimes the same code should be able to work with tensors of different dimensionalities.
In this case, we can use .. to collectively designate any existing
dimensions not explicitly referenced.
For example, say we want to index into the first dimension of whatever
tensor is passed, be it a matrix, an array, or some
higher-dimensional structure. The following
t1 <- torch_randn(2, 2)
t2 <- torch_randn(2, 2, 2)
t3 <- torch_randn(2, 2, 2, 2)
t1[1, ..]
## torch_tensor
## 1.1376
## 2.3105
## [ CPUFloatType{2} ]
t2[1, ..]
## torch_tensor
## -1.1752 -0.3022
## 0.8728 0.2683
## [ CPUFloatType{2,2} ]
t3[1, ..]
## torch_tensor
## (1,.,.) =
## -0.0562 1.2800
## -0.1790 -0.8129
##
## (2,.,.) =
## 1.0048 -2.3087
## -1.4101 0.1139
## [ CPUFloatType{2,2,2} ]
If we wanted to index into the last dimension instead, we’d write
t[.., 1]. We can even combine both:
t3[1, .., 2]
## torch_tensor
## 1.2800 -0.8129
## -2.3087 0.1139
## [ CPUFloatType{2,2} ]
10.5. Reshaping tensors#
We can modify a tensor’s shape, without juggling around its values,
using the view() method
Here is the initial tensor, a vector of length 24:
t <- torch_zeros(24)
print(t, n = 3)
## torch_tensor
## 0
## 0
## 0
## ... [the output was truncated (use n=-1 to disable)]
## [ CPUFloatType{24} ]
Here is that same vector, reshaped to a wide matrix:
t2 <- t$view(c(2, 12))
t2
## torch_tensor
## 0 0 0 0 0 0 0 0 0 0 0 0
## 0 0 0 0 0 0 0 0 0 0 0 0
## [ CPUFloatType{2,12} ]
Whenever we ask torch to perform an operation that changes the shape
of a tensor, it tries to fulfill the request without allocating new
storage for the tensor’s contents.
How does torch do it? Let’s see a concrete example. We start with a 3
x 5 matrix.
t <- torch_tensor(matrix(1:15, nrow = 3, byrow = TRUE))
t
## torch_tensor
## 1 2 3 4 5
## 6 7 8 9 10
## 11 12 13 14 15
## [ CPULongType{3,5} ]
Tensors have a stride() method that tracks, for every dimension, how
many elements have to be traversed to arrive at its next element.
For the above tensor t, to go to the next row, we have to skip over
five elements, while to go to the next column, we need to skip just
one:
t$stride()
## [1] 5 1
Now we reshape the tensor so it has five rows and three columns
instead. Remember, the data themselves do not change.
t2 <- t$view(c(5, 3))
t2
## torch_tensor
## 1 2 3
## 4 5 6
## 7 8 9
## 10 11 12
## 13 14 15
## [ CPULongType{5,3} ]
t2$stride()
## [1] 3 1
This time, to arrive at the next row, we just skip three elements instead of five. To get to the next column, we still just “jump over” a single element only:
10.6. Broadcasting#
Multiply every element by a scalar. This works:
t1 <- torch_randn(3, 5)
t1 * 0.5
## torch_tensor
## 0.0130 -0.0835 0.6924 0.6262 0.1971
## -0.5043 -0.9089 0.1011 -0.4738 -0.6423
## 0.2129 0.3098 -0.3925 0.3697 -0.2689
## [ CPUFloatType{3,5} ]
Add the same vector to every row in a matrix
m <- matrix(1:15, ncol = 5, byrow = TRUE)
m2 <- matrix(1:5, ncol = 5, byrow = TRUE)
# m + m2
## Error in m + m2 : non-conformable arrays
Neither does it help if we make m2 a vector.
m3 <- 1:5
m + m3
## [,1] [,2] [,3] [,4] [,5]
## [1,] 2 6 5 9 8
## [2,] 8 12 11 10 14
## [3,] 14 13 17 16 20
