Ctrl+K

Dimension Reduction

6. Dimension Reduction#

6.1. Dimension Reduction Techniques#

Dimension reduction techniques aim to reduce the number of predictors by transforming them into a lower-dimensional space while preserving most of the variability in the data.

  • Dimension reduction techniques are effective for dealing with multicollinearity and high-dimensional data

  • The goal is constructing \(M\) new predictors, which are linear combination of \(p\) original predictors, and use the new predictors to make predictions.

    • Let \(Z_1,Z_2,...,Z_M\) represent the new predictors with \(M<P\)

    • \(\phi_{m1},...,\phi_{mj}\) are some constants $\( Z_m = \sum_{j=1}^{p}\phi_{mj}X_j \)$

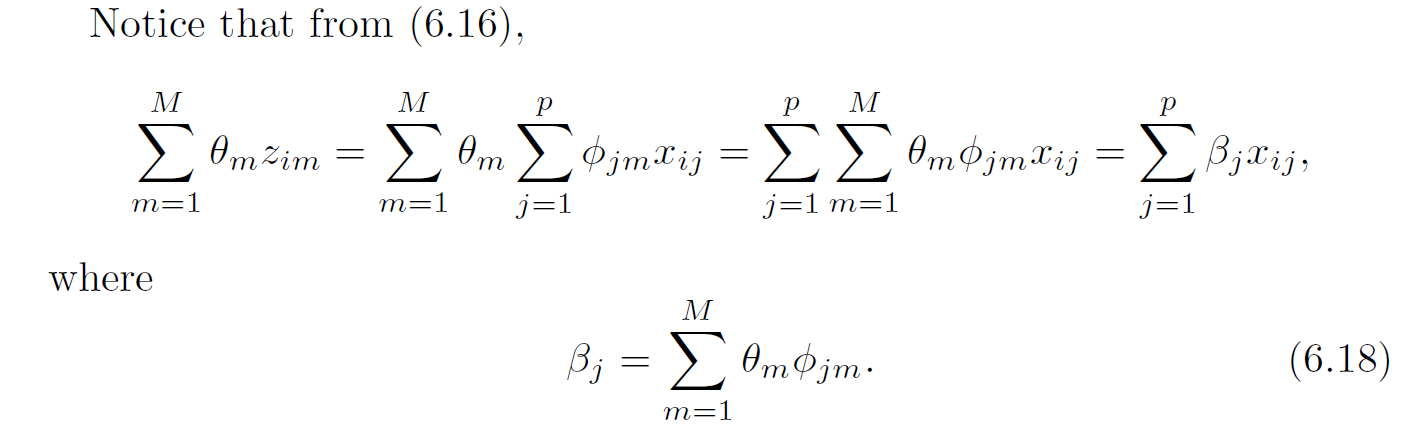
    • Then we fit * \(i=1,...,n\) $\( y_i = \theta_0+\sum_{m=1}^{M}\theta_mZ_{im} + e_i \)$ image-2.png

  • But may result in less interpretable models compared to subset selection and shrinkage methods.

6.1.1. Principal Component Analysis#

  • PCA transforms the original predictors into a new set of uncorrelated variables called principal components.

  • These components are ordered by the amount of variance they explain, allowing for dimensionality reduction by retaining only the most important components.

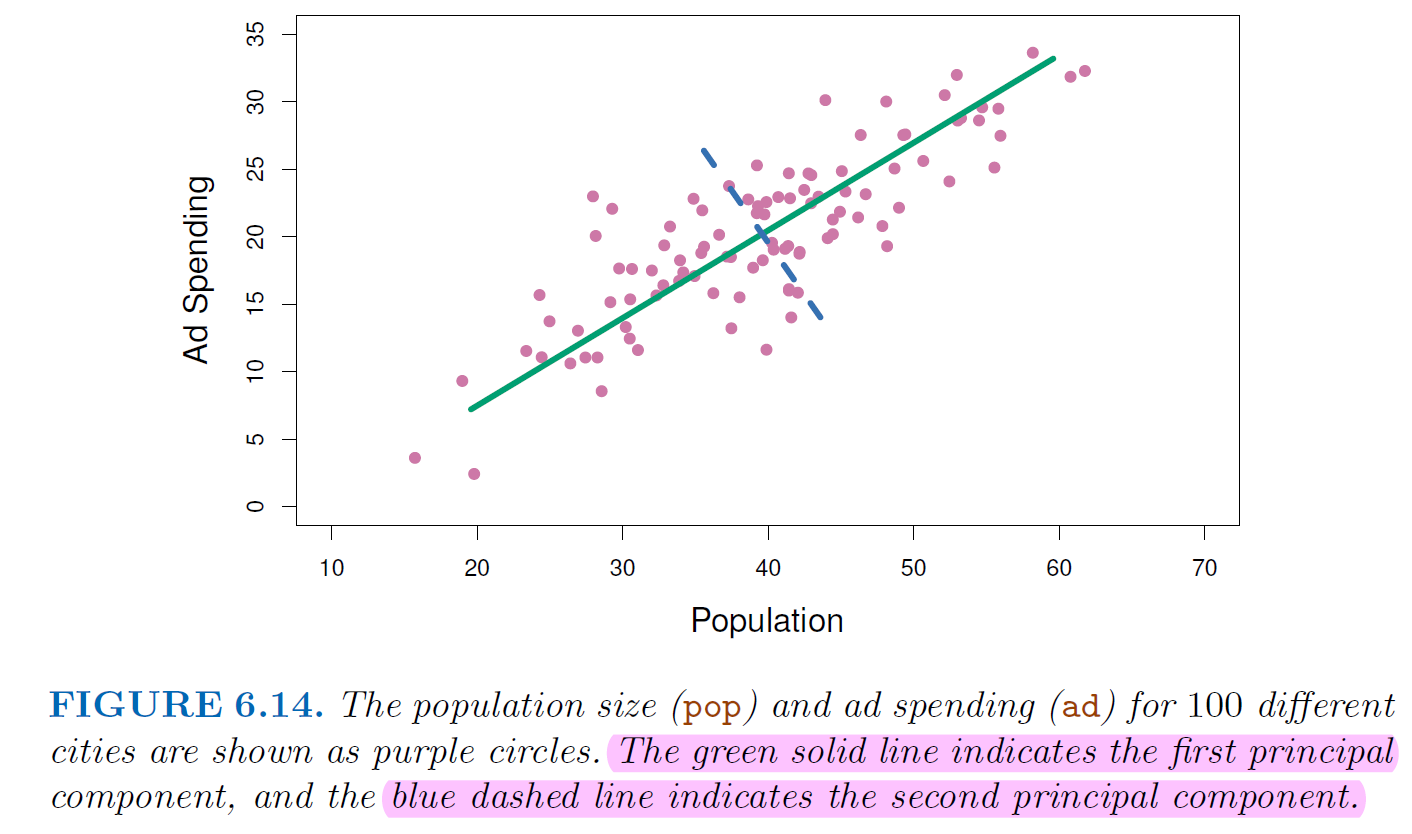
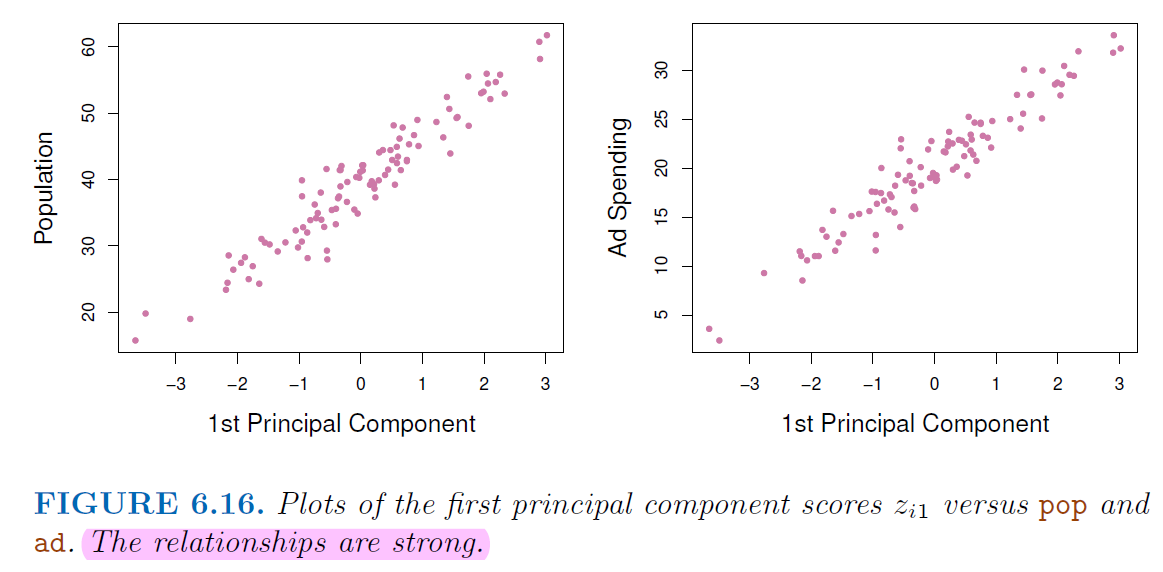
image-2.png

  • The first component summarize the most information from these two features

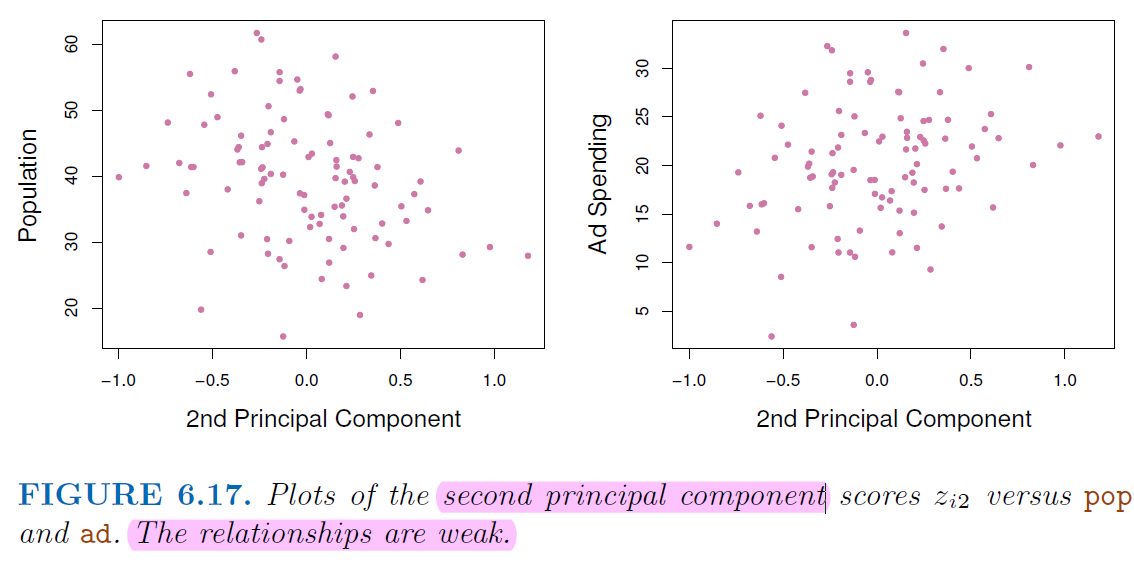
image-2.png

  • Not many information left on the 2nd component

image-2.png

6.1.2. Partial Least Squares (PLS)#

  • PCR assumes the principle components from predictors might have the best performance on dependent variable prediction (unsupervised way)

    • This assumption might wrong

    • We do not use the information from dependent variable to supervise the identification of the principal components.

  • PLS is also a dimension reduction technique

    • But unlike PCR, PLS identify new features that not only approximate the old features well, but also that are related to the target variable

    • Steps:

      1. Standardize \(p\) predictors

      2. Construct simple Bivariate linear regression to get \(\theta_1,...,\theta_p\)

      3. Compute the first direction \(Z_1=\sum_{j=1}^p\theta_1jX_j\)

        1. PLS places the highest weight on the variables that most strongly related to the response.

Contents