Ctrl+K

Regression

2. Regression#

2.1. Simple Linear Regression#

\(Y=\beta_0+\beta_1 x + e\)

  • \(Y\) represents the dependent variable or the variable we are trying to predict or explain.

  • \(x\) represents the independent variable or the predictor variable.

  • \(\beta_0\) is the intercept of the regression line, which is the predicted value of \(Y\) when \(x\) is zero.

  • \(\beta_1\) is the slope of the regression line, representing the average change in \(Y\) for a one-unit change in \(x\).

  • \(e\) stands for the error term (also known as the residual), which is the difference between the observed values and the values predicted by the model.

image.png

# Import necessary libraries
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# Generate some random data for demonstration
np.random.seed(0) # Seed for reproducibility
x = np.random.rand(100, 1) # 100 random numbers for independent variable
y = 2 + 3 * x + np.random.randn(100, 1) # Dependent variable with some noise

# Create a linear regression model
model = LinearRegression()

# Fit the model with our data (x - independent, y - dependent)
model.fit(x, y)

# Print the coefficients
print("Intercept (beta_0):", model.intercept_)
print("Slope (beta_1):", model.coef_)

Intercept (beta_0): [2.22215108]
Slope (beta_1): [[2.93693502]]

# Use the model to make predictions
y_pred = model.predict(x)

# Plotting
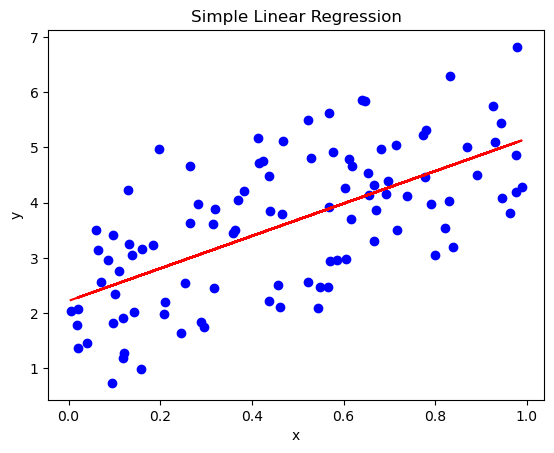
plt.scatter(x, y, color='blue') # actual data points
plt.plot(x, y_pred, color='red') # our model's predictions
plt.title('Simple Linear Regression')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
../../_images/1831aafd86aa4f5485189a6e0ce102e4fa2c052916aacc37e9cac78a7e00ab36.png

2.1.1. Find Best estimator of \(\beta_1\)#

2.1.1.1. Ordinary Least Squares#

  • The goal is to find the values of \(\beta_0\) and \(\beta_1\) that minimize the sum of the squared differences (residuals) between the observed values and the values predicted by the linear model.

  • \(Minimize(e) = (\sum (y_i-(\beta_0+\beta_1 x_i))^2)\), where \(y_i\) and \(x_i\) are the observed values.

  • Steps to calculate it

  1. Calculate the partial derivatives of intercept \(\beta_0\) and let it equal to 0

    • \(\frac{\partial e}{\partial \beta_0}=\sum_i 2(y_i-\beta_0-\beta_i x_i)(-1) = 0\)

    • \(\frac{\partial e}{\partial \beta_0}= \sum_i \beta_1 x_i -n*\beta_0 -\sum_i y_i =0\)

    • \(\sum_i \beta_1 x_i +n*\beta_0 -\sum_i y_i =0 \to n*\beta_1\bar x +n*\beta_0-n*\bar y = 0\)

    • \( n*\beta_1\bar x +n*\beta_0-n\*\bar y = 0 \to \beta_1\bar x + \beta_0-\bar y = 0\)

    • \(\beta_1\bar x + \beta_0-\bar y = 0 \to \beta_0=\bar y - \beta_1 \bar x\)

  2. Calculate the partial derivative of slope \(\beta_1\) and let it equal to 0

    • \(\frac{\partial e}{\partial \beta_1} = \sum_i2(y_i-\beta_1 x_i -\beta_0) (-x_i) =0\)

    • \(\sum_i2(y_i-\beta_1 x_i -\beta_0) (-x_i) =0 \to \sum_i(\beta_1x_i^2+\beta_0 x_i -x_i y_i)=0\)

    • Replace \(\beta_0\) with \((\bar y - \beta_1 \bar x)\) : \(\sum_i(\beta_1x_i^2+(\bar y -\beta_1 \bar x) x_i -x_i y_i)=0\)

    • \(\beta_1(\sum_i x_iy_i-\bar y \sum_i x_i) = \sum_i x_i^2-\bar x\sum_i x_i \to \beta_1 = \frac{\sum_i x_iy_i-\bar y \sum_i x_i}{\sum_i x_i^2-\bar x\sum_i x_i}\)

    • According to the Summation Property (As shown below):

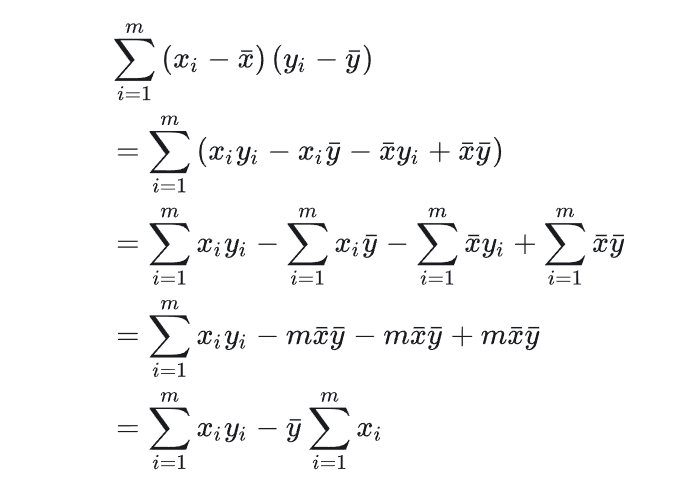
    image.png

    • We will have \(\beta_1=\frac{Cov(X,Y)}{Var(X)}\)

2.1.2. Assessing the Accuracy of Coefficient Estimates#

  • \(SE(\beta_1)^2 = \frac{\sigma^2}{\sum_{i=1}^{n}(x-\bar x)^2}\)

  • \(SE(\beta_0)^2 = \sigma^2[\frac{1}{n}+\frac{\bar x^2}{\sum_{i=1}^n(x_i-\bar x)^2}]\)

    • Where \(\sigma^2 = Var(e)\)

  • These two standard errors can be used to compute confidence interval, for example, for 95% confidence interval, it has the form [\(\beta_1 - 2*SE(\beta_1)\), \(\beta_1 + 2*SE(\beta_1)\)]

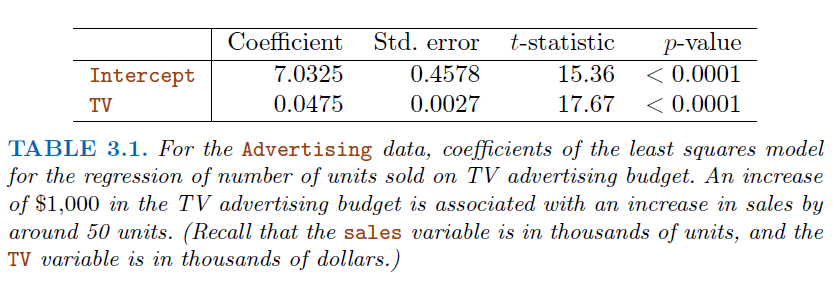
2.1.3. Hypothesis Testing#

  • Standard errors can be used to perform hypothesis tests on coefficients.

  • To test the null hypothesis, we compute a t-statistic, given by
    \(t=\frac{\beta_1-0}{SE(\beta_1)}\)

    • This value follows a t-distribution with n-2 degrees of freedom

    • \(H_0\) assumes \(\beta_1 = 0\)

    • Since \(H_0:\beta_1 = 0\), [\(\beta_1 - 2*SE(\beta_1)\), \(\beta_1 + 2*SE(\beta_1)\)] should not contain 0

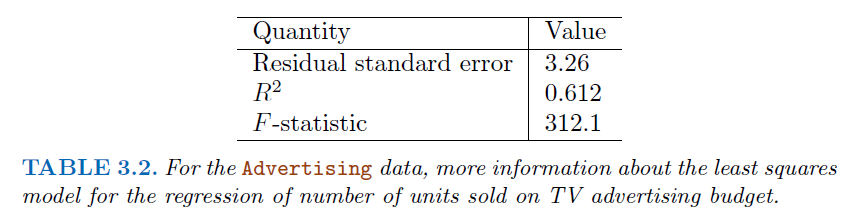
image.png

2.1.4. Assessing the Overall Accuracy of the Model#

  • We compute the Residual Standard Error

    \(RSE = \sqrt{\frac{1}{n-2}RSS} = \sqrt{\frac{1}{n-2}\sum_i^n(y_i-\hat y_i)^2}\)

    • Where RSS is the residual sum-of-squares

  • We can also use R-squared (fraction of variance explained):

    \(R^2 = \frac{TSS-RSS}{TSS}=1-\frac{RSS}{TSS}\)

    • Where \( TSS=\sum\_{i=1}^n(y_i -\bar y)^2\), is the total sum of squares

    • Also, In the simple linear regression setting, \(R^2 = r^2\) where \(r\) is the correlation between \(X\) and \(Y\):

    \(r=\frac{\sum_{i=1}^2(x_i-\bar x)(y_i-\bar y)}{\sqrt{\sum_{i=1}^2(x_i-\bar x)^2}\sqrt{\sum_{i=1}^2(y_i-\bar y)^2}}\)

    image.png

# Example data
x = np.array([1., 2., 3., 4., 5.]).reshape(-1, 1)
y = np.array([2., 4., 5., 8., 7.])

# Calculating means
x_mean = np.mean(x)
y_mean = np.mean(y)

# Calculating Beta_1
numerator = sum([i*j for i,j in zip(x-x_mean,y-y_mean)])
denominator = np.sum((x - x_mean)**2)
beta_1 = numerator / denominator

print("Beta_1 (slope) using OLS:", beta_1)

Beta_1 (slope) using OLS: [1.4]

2.1.5. Maximum likelihood estimation#

  • In the context of linear regression, MLE assumes that the residuals (differences between observed and predicted values) are normally distributed.

  • The method finds the parameter values that maximize the likelihood of observing the given data.

2.2. Multiple Linear Regression#

\(Y=\beta_0+\beta_1 X_1+\beta_2 X_2+...+\beta_p X_p + e\)

  • Correlations amongst predictors cause problems (multicollinearity):

    • The variance of all coefficient tends to increase, sometimes dramatically.

    • \(t=\frac{\beta_1-0}{SE(\beta_1)}\), If \(SE(\beta_1)\) becomes larger, will contributes to a \(t\) closer to 0, which will lead to a larger p-value

    • Also, it’s hard to interpret.

  • Claims of causality should be avoided!

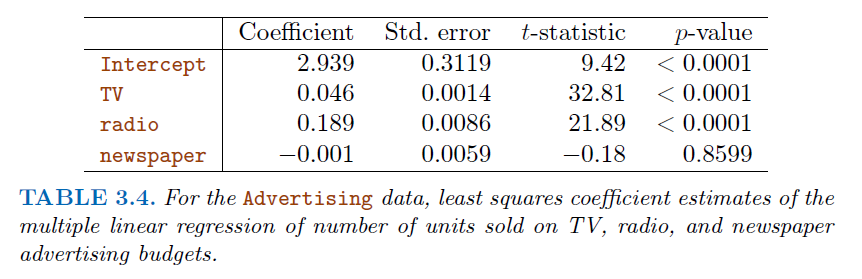
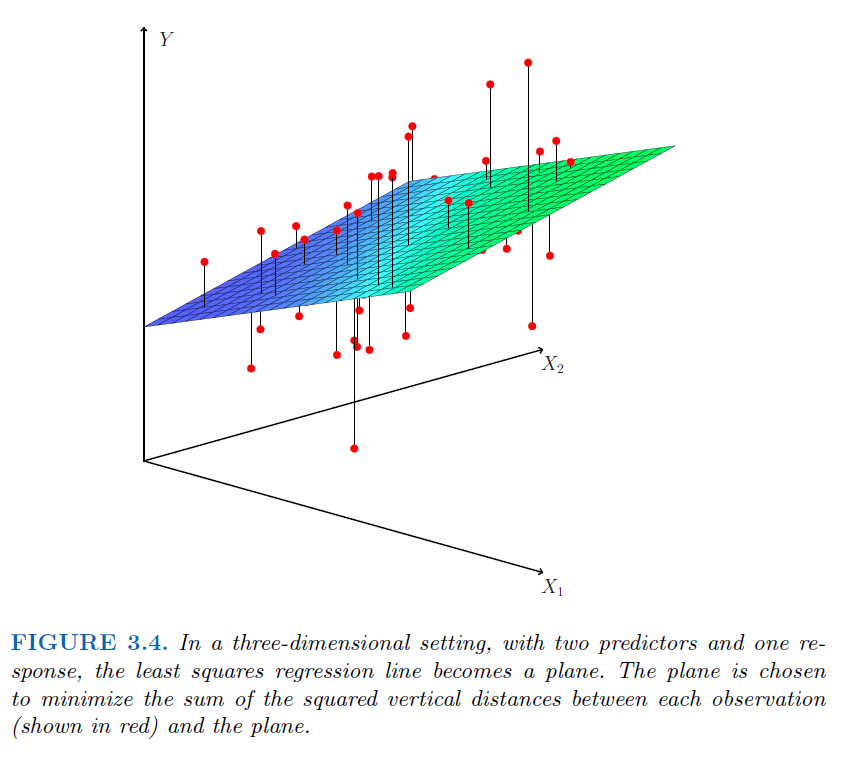
image.png

image.png

2.2.1. Important Question (Hypothesis testing)#

  1. Is at least one of the predictors \(X_1,X_2,...,X_p\) useful in predicting the response?

    • For this question, we use the \(F-statistic\)

    • \(F=\frac{(TSS-RSS)/p}{RSS/(n-p-1)}\)~\(F_{p,n-p-1}\)

      • Where \(n\) is the number of observations, \(p\) is the number of predictors

    • \(H_0:\) None of these predictors are useful

    image.png

    • If \(H_0\) is false, we expect \(F>1\)

  2. Do all the predictors help to explain \(Y\), or is only a subset of the predictors useful?

    • Forward Selection

      • Begin with the null model

      • Fit p simple linear regression and add the null model the variable results in the lowest RSS

      • Add to that model the variable that results in the lowest RSS amongst all two-variable models.

      • Continue until stopping rules is satisfied (e.g. p-value >0.05 for all remaining variables)

    • Backward Selection

    image.png

    • Model Selection

      • Besides RSS, there are some other criteria for choosing an “optimal” member in stepwise searching, including Akaike information criterion (AIC), Bayesian information criterion (BIC), adjusted R-squared

  3. How well does the model fit the data?

  4. Given a set of predictor values, what response value should we predict, and how accurate is our prediction?

2.2.2. Polynomial regression (non-linear effects)#

image.png

image.png

2.3. Interesting Quotes by famous Statisticians#

  • Essentially, all models are wrong, but some are useful

    • George Box

  • The only way to find out what will happen when a complex system is disturbed is to disturb the system, not merely to observe it passively

    • Fred Mosteller and John Tukey, paraphrasing George Box

Contents